Voigtprofil
 | Den här artikeln behöver källhänvisningar för att kunna verifieras. (2012-10) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan. |
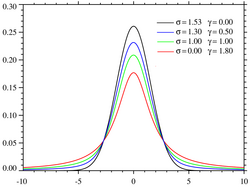
En Voigtprofil är en sorts hopslagning, faltning eller konvolution, av en Gausskurva med en Lorentzkurva, som är vanlig inom spektroskopi.
Där är Voigtprofilen en spektrallinjeprofil uppkallad efter Woldemar Voigt och uppträder inom alla grenar av spektroskopi i vilken en spektrallinje blir breddad av två sorters mekanismer, av vilka den ena för sig skulle ge en Gaussprofil (ofta som ett resultat av Dopplerbreddning), medan den andra skulle leda till en Lorentzprofil. Alla normerade linjeprofiler kan anses vara sannolikhetsfördelningar.
Gauss-profilen är ekvivalent med en Gauss- eller normalfördelning och en Lorentzprofil är ekvivalent med en Lorentz- eller Cauchy- fördelning. Utan att förlora i allmängiltighet, kan vi nöja oss att beakta centrerade profiler som har maximum vid noll. Voigtprofilen är då en faltning av en Lorentzprofil och en Gaussprofil:
där x är frekvens från linjens mitt, är den centrerade Gaussprofilen:
och L(x; γ) är den centrerade Lorentzprofilen:
Den definierande integralen kan evalueras som:
där Re[w(z)] är den reella delen av komplexa felfunktionen av z och




![{\displaystyle V(x;\sigma ,\gamma )={\frac {{\textrm {Re}}[w(z)]}{\sigma {\sqrt {2\pi }}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d353eb39c4dd9c7709a4160cad4cf79e812689ab)










