Magnitude absoluta

A magnitude absoluta (M) é uma medida da luminosidade de um objeto astronômico em uma escala de magnitude astronômica logarítmica inversa. A magnitude absoluta de um objeto é definida como igual à magnitude aparente que o objeto teria se fosse visto de uma distância de exatamente 10 parsecs (32.6 anos-luz), sem extinção (ou escurecimento) de sua luz devido à absorção pela matéria interestelar e poeira cósmica. Ao colocar hipoteticamente todos os objetos a uma distância de referência padrão do observador, suas luminosidades podem ser comparadas diretamente entre si em uma escala de magnitude.

Assim como todas as magnitudes astronômicas, a magnitude absoluta pode ser especificada para diferentes faixas de comprimento de onda correspondentes a bandas de filtro ou bandas passantes especificadas; para estrelas, uma magnitude absoluta comumente citada é a magnitude visual absoluta, que usa a banda visual (V) do espectro (no sistema fotométrico UBV). As magnitudes absolutas são indicadas por um M maiúsculo, com um subscrito representando a faixa de filtro usada para medição, como M_V para magnitude absoluta na banda V.

Quanto mais luminoso um objeto, menor o valor numérico de sua magnitude absoluta. Uma diferença de 5 magnitudes entre as magnitudes absolutas de dois objetos corresponde a uma razão de 100 em suas luminosidades, e uma diferença de n magnitudes em magnitude absoluta corresponde a uma razão de luminosidade de 100^n/5. Por exemplo, uma estrela de magnitude absoluta M_V = 3.0 seria 100 vezes mais luminosa que uma estrela de magnitude absoluta M_V = 8.0 medida na banda do filtro V. O Sol tem magnitude absoluta M_V = +4.83.^[1] Objetos altamente luminosos podem ter magnitudes absolutas negativas: por exemplo, a Via Láctea tem uma magnitude B absoluta de cerca de −20.8.^[2]

A magnitude bolométrica absoluta (M_bol) de um objeto representa sua luminosidade total em todos os comprimentos de onda, em vez de em uma única faixa de filtro, conforme expresso em uma escala de magnitude logarítmica. Para converter de uma magnitude absoluta em uma banda de filtro específica para magnitude bolométrica absoluta, uma correção bolométrica (BC) é aplicada.^[3]

Para corpos do Sistema Solar que brilham na luz refletida, uma definição diferente de magnitude absoluta (H) é usada, com base em uma distância de referência padrão de uma unidade astronômica.

Estrelas e galáxias

Na astronomia estelar e galáctica, a distância padrão é de 10 parsecs (cerca de 32.616 anos-luz, 308.57 petametros ou 308.57 trilhões de quilômetros). Uma estrela em 10 parsecs tem uma paralaxe de 0.1″ (100 milisegundos de arco). Galáxias (e outros objetos extensos) são muito maiores do que 10 parsecs, sua luz é irradiada sobre um trecho estendido do céu e seu brilho geral não pode ser observado diretamente de distâncias relativamente curtas, mas a mesma convenção é usada. A magnitude de uma galáxia é definida medindo toda a luz irradiada sobre todo o objeto, tratando esse brilho integrado como o brilho de uma única fonte pontual ou estrela, e calculando a magnitude dessa fonte pontual como ela apareceria se observado na distância padrão de 10 parsecs. Consequentemente, a magnitude absoluta de qualquer objeto é igual à magnitude aparente que teria se estivesse a 10 parsecs de distância.

Algumas estrelas visíveis a olho nu têm uma magnitude absoluta tão baixa que pareceriam brilhantes o suficiente para ofuscar os planetas e projetar sombras se estivessem a 10 parsecs da Terra. Os exemplos incluem Rígel (−7.0), Deneb (−7.2), Naos (−6.0) e Betelgeuse (−5.6). Para comparação, Sirius tem uma magnitude absoluta de apenas 1.4, que ainda é mais brilhante que o Sol, cuja magnitude visual absoluta é de 4.83. A magnitude bolométrica absoluta do Sol é definida arbitrariamente, geralmente em 4.75.^[4][5] As magnitudes absolutas das estrelas geralmente variam de aproximadamente −10 a +20. As magnitudes absolutas das galáxias podem ser muito menores (mais brilhantes). Por exemplo, a galáxia elíptica gigante Messier 87 tem uma magnitude absoluta de −22 (ou seja, tão brilhante quanto cerca de 60.000 estrelas de magnitude −10). Alguns núcleos galácticos ativos (quasares como CTA-102) podem atingir magnitudes absolutas superiores a −32, tornando-os os objetos persistentes mais luminosos no universo observável, embora esses objetos possam variar em brilho em escalas de tempo astronomicamente curtas. No extremo, o brilho óptico da erupção de raios gama GRB 080319B atingiu, de acordo com um artigo, uma magnitude r absoluta mais brilhante que −38 por algumas dezenas de segundos.^[6]

Magnitude aparente

O astrônomo grego Hiparco estabeleceu uma escala numérica para descrever o brilho de cada estrela que aparece no céu. As estrelas mais brilhantes no céu receberam uma magnitude aparente m = 1, e as estrelas mais fracas visíveis a olho nu receberam uma magnitude m = 6.^[7] A diferença entre eles corresponde a um fator de 100 no brilho. Para objetos na vizinhança imediata do Sol, a magnitude absoluta M e a magnitude aparente m de qualquer distância d (em parsecs, com 1 pc = 3.2616 anos-luz) são relacionadas por

onde F é o fluxo radiante medido na distância d (em parsecs), F₁₀ o fluxo radiante medido na distância 10 pc. Usando o logaritmo comum, a equação pode ser escrita como

onde é assumido que a extinção de gás e poeira é insignificante. As taxas de extinção típicas dentro da Via Láctea são de 1 a 2 magnitudes por kiloparsec, quando as nuvens escuras são levadas em conta.^[8]

Para objetos a distâncias muito grandes (fora da Via Láctea) a distância de luminosidade d_L (distância definida usando medições de luminosidade) deve ser usada em vez de d, porque a aproximação euclidiana é inválida para objetos distantes. Em vez disso, a relatividade geral deve ser levada em conta. Além disso, o desvio para o vermelho cosmológico complica a relação entre magnitude absoluta e aparente, porque a radiação observada foi deslocada para a faixa vermelha do espectro. Para comparar as magnitudes de objetos muito distantes com as de objetos locais, pode ser necessário aplicar uma correção K às magnitudes dos objetos distantes.

A magnitude absoluta M também pode ser escrita em termos da magnitude aparente m e da paralaxe estelar p:

ou usando magnitude aparente m e módulo de distância μ:

Exemplos

Rígel tem uma magnitude visual m_V de 0.12 e distância de cerca de 860 anos-luz:

Vega tem uma paralaxe p de 0.129″ e uma magnitude aparente m_V de 0.03:

A Galáxia Olho Negro tem uma magnitude visual m_V de 9.36 e um módulo de distância μ de 31.06:

Magnitude bolométrica

A magnitude absoluta bolométrica M_bol, leva em conta a radiação eletromagnética em todos os comprimentos de onda. Inclui aqueles não observados devido à banda passante instrumental, à absorção atmosférica da Terra e à extinção pela poeira interestelar. É definido com base na luminosidade das estrelas. No caso de estrelas com poucas observações, deve ser calculado assumindo uma temperatura efetiva.

Classicamente, a diferença de magnitude bolométrica está relacionada com a razão de luminosidade de acordo com:^[7]

que faz por inversão:

onde

• L_⊙ é a luminosidade do Sol (luminosidade bolométrica)
• L_★ é a luminosidade da estrela (luminosidade bolométrica)
• M_bol,⊙ é a magnitude bolométrica do Sol.
• M_bol,★ é a magnitude bolométrica da estrela.

Em agosto de 2015, a União Astronômica Internacional (IAU) aprovou a Resolução B2^[9] definindo os pontos zero das escalas de magnitude bolométrica absoluta e aparente em unidades SI para potência (watts) e irradiância (W/m²), respectivamente. Embora as magnitudes bolométricas tenham sido usadas pelos astrônomos por muitas décadas, houve diferenças sistemáticas nas escalas de magnitude absoluta-luminosidade apresentadas em várias referências astronômicas e nenhuma padronização internacional. Isso levou a diferenças sistemáticas nas escalas de correções bolométricas.^[10] Combinado com magnitudes bolométricas absolutas incorretas assumidas para o Sol, isso pode levar a erros sistemáticos nas luminosidades estelares estimadas (e outras propriedades estelares, como raios ou idades, que dependem da luminosidade estelar para serem calculadas).

A resolução B2 define uma escala de magnitude bolométrica absoluta onde M_bol = 0 corresponde à luminosidade L₀ = 7028301280000000000♠3.0128×10²⁸ W, com a luminosidade do ponto zero L₀ definida de modo que o Sol (com luminosidade nominal 7026382800000000000♠3.828×10²⁶ W) corresponda à magnitude bolométrica absoluta M_bol,⊙ = 4.74. Colocando uma fonte de radiação (por exemplo, estrela) na distância padrão de 10 parsecs, segue-se que o ponto zero da escala de magnitude bolométrica aparente m_bol = 0 corresponde à irradiância f₀ = 6992251802100199999♠2.518021002×10⁻⁸ W/m². Usando a escala IAU 2015, a irradiância solar nominal total ("constante solar") medida em 1 unidade astronômica (7003136100000000000♠1361 W/m²) corresponde a uma magnitude bolométrica aparente do Sol de m_bol,⊙ = −26.832.^[10]

Seguindo a Resolução B2, a relação entre a magnitude bolométrica absoluta de uma estrela e sua luminosidade não está mais diretamente ligada à luminosidade (variável) do Sol:

onde

• L_★ é a luminosidade da estrela (luminosidade bolométrica) em watts
• L₀ é a luminosidade do ponto zero 7028301280000000000♠3.0128×10²⁸ W
• M_bol é a magnitude bolométrica da estrela

A nova escala de magnitude absoluta da IAU desconecta permanentemente a escala da variável Sol. No entanto, nesta escala de potência do SI, a luminosidade solar nominal corresponde aproximadamente a M_bol = 4.74, um valor que era comumente adotado pelos astrônomos antes da resolução da IAU de 2015.^[10]

A luminosidade da estrela em watts pode ser calculada em função de sua magnitude bolométrica absoluta M_bol como:

usando as variáveis definidas anteriormente.

Corpos do Sistema Solar (H)

Magnitude absoluta (H)
e diâmetro para
asteróides
(albedo=0.14)^[11]

H	Diâmetro
10	36 km
12.7	10 km
15	3.6 km
17.7	1 km
19.2	510 m
20	360 m
22	140 m
22.7	100 m
24.2	51 m
25	36 m
26.6	17 m
27.7	10 m
30	3.6 m
32.7	1 m

Para planetas e asteroides, é usada uma definição de magnitude absoluta que é mais significativa para objetos não estelares. A magnitude absoluta, comumente chamada de ${\displaystyle H}$, é definida como a magnitude aparente que o objeto teria se estivesse a uma unidade astronômica (UA) do Sol e do observador, e em condições de oposição solar ideal (um arranjo que é impossível na prática).^[12] Como os corpos do Sistema Solar são iluminados pelo Sol, seu brilho varia em função das condições de iluminação, descritas pelo ângulo de fase. Essa relação é chamada de curva de fase. A magnitude absoluta é o brilho no ângulo de fase zero, um arranjo conhecido como oposição, a uma distância de uma UA.

Magnitude aparente

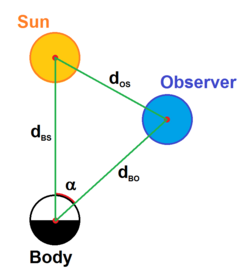
A magnitude absoluta ${\displaystyle H}$ pode ser usada para calcular a magnitude aparente ${\displaystyle m}$ de um corpo. Para um objeto refletindo a luz solar, ${\displaystyle H}$ e ${\displaystyle m}$ são conectados pela relação

onde ${\displaystyle \alpha }$ é o ângulo de fase, o ângulo entre as linhas corpo-sol e corpo-observador. ${\displaystyle q(\alpha )}$ é a integral de fase (a integração da luz refletida; um número na faixa de 0 a 1).^[13]

Pela lei dos cossenos, temos:

Distâncias:

• d_BO é a distância entre o corpo e o observador
• d_BS é a distância entre o corpo e o Sol
• d_OS é a distância entre o observador e o Sol
• d₀, um fator de conversão de unidade, é a constante 1 UA, a distância média entre a Terra e o Sol

Aproximações para integral de fase q(α)

O valor de ${\displaystyle q(\alpha )}$ depende das propriedades da superfície refletora, em particular de sua rugosidade. Na prática, diferentes aproximações são usadas com base nas propriedades conhecidas ou assumidas da superfície. As superfícies dos planetas terrestres são geralmente mais difíceis de modelar do que as dos planetas gasosos, os últimos dos quais têm superfícies visíveis mais suaves.^[13]

Planetas como esferas difusas

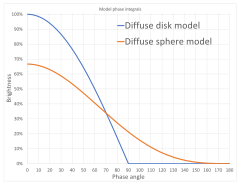
Os corpos planetários podem ser aproximados razoavelmente bem como esferas refletoras difusas ideais. Seja ${\displaystyle \alpha }$ o ângulo de fase em graus, então^[14]

Uma esfera difusa de fase completa reflete dois terços da luz que um disco plano difuso do mesmo diâmetro. Um quarto de fase (${\displaystyle \alpha =90^{\circ }}$) tem ${\textstyle {\frac {1}{\pi }}}$ tanta luz quanto a fase completa (${\displaystyle \alpha =0^{\circ }}$).

Por outro lado, um modelo de disco refletor difuso é simplesmente ${\displaystyle q(\alpha )=\cos {\alpha }}$, o que não é realista, mas ele representa o aumento de oposição para superfícies ásperas que refletem luz mais uniforme de volta em ângulos de fase baixos.

A definição do albedo geométrico ${\displaystyle p}$, uma medida para a refletividade das superfícies planetárias, é baseada no modelo do disco refletor difuso. A magnitude absoluta ${\displaystyle H}$, o diâmetro ${\displaystyle D}$ (em quilômetros) e o albedo geométrico ${\displaystyle p}$ de um corpo são relacionados por^[15][16][17]

Exemplo: a magnitude absoluta da Lua ${\displaystyle H}$ pode ser calculada a partir de seu diâmetro ${\displaystyle D=3474{\text{ km}}}$ e albedo geométrico ${\displaystyle p=0.113}$:^[18]

Temos ${\displaystyle d_{BS}=1{\text{ UA}}}$, ${\displaystyle d_{BO}=384400{\text{ km}}=0.00257{\text{ UA}}.}$ No quarto de fase, ${\textstyle q(\alpha )\approx {\frac {2}{3\pi }}}$ (de acordo com o modelo do refletor difuso), isso produz uma magnitude aparente de ${\textstyle m=+0.28+5\log _{10}{\left(1\cdot 0.00257\right)}-2.5\log _{10}{\left({\frac {2}{3\pi }}\right)}=-10.99.}$ O valor real é um pouco menor do que isso, ${\displaystyle m=-10.0.}$ A curva de fase da Lua é muito complicada para o modelo de refletor difuso.^[19] Uma fórmula mais precisa é fornecida na seção a seguir.

Modelos mais avançados

Como os corpos do Sistema Solar nunca são refletores difusos perfeitos, os astrônomos usam modelos diferentes para prever magnitudes aparentes com base em propriedades conhecidas ou assumidas do corpo.^[13] Para planetas, aproximações para o termo de correção ${\displaystyle -2.5\log _{10}{q(\alpha )}}$ na fórmula para m foram derivados empiricamente, para coincidir com as observações em diferentes de ângulos de fase. As aproximações recomendadas pelo Astronomical Almanac^[20] são (com ${\displaystyle \alpha }$ em graus):

Planeta	${\displaystyle H}$	Aproximação para ${\displaystyle -2.5\log _{10}{q(\alpha )}}$
Mercúrio	−0.613	${\displaystyle +6.328\times 10^{-2}\alpha -1.6336\times 10^{-3}\alpha ^{2}+3.3644\times 10^{-5}\alpha ^{3}-3.4265\times 10^{-7}\alpha ^{4}+1.6893\times 10^{-9}\alpha ^{5}-3.0334\times 10^{-12}\alpha ^{6}}$
Vênus	−4.384	${\displaystyle -1.044\times 10^{-3}\alpha +3.687\times 10^{-4}\alpha ^{2}-2.814\times 10^{-6}\alpha ^{3}+8.938\times 10^{-9}\alpha ^{4}}$ (para ${\displaystyle 0^{\circ }<\alpha \leq 163.7^{\circ }}$) ${\displaystyle +240.44228-2.81914\alpha +8.39034\times 10^{-3}\alpha ^{2}}$ (para ${\displaystyle 163.7^{\circ }<\alpha <179^{\circ }}$)
Terra	−3.99	${\displaystyle -1.060\times 10^{-3}\alpha +2.054\times 10^{-4}\alpha ^{2}}$
Lua[21]	+0.28	${\displaystyle +2.9994\times 10^{-2}\alpha -1.6057\times 10^{-4}\alpha ^{2}+3.1543\times 10^{-6}\alpha ^{3}-2.0667\times 10^{-8}\alpha ^{4}+6.2553\times 10^{-11}\alpha ^{5}}$ (para ${\displaystyle \alpha \leq 150^{\circ }}$, antes da lua cheia) ${\displaystyle +3.3234\times 10^{-2}\alpha -3.0725\times 10^{-4}\alpha ^{2}+6.1575\times 10^{-6}\alpha ^{3}-4.7723\times 10^{-8}\alpha ^{4}+1.4681\times 10^{-10}\alpha ^{5}}$ (para ${\displaystyle \alpha \leq 150^{\circ }}$, depois da lua cheia)
Marte	−1.601	${\displaystyle +2.267\times 10^{-2}\alpha -1.302\times 10^{-4}\alpha ^{2}}$ (para ${\displaystyle 0^{\circ }<\alpha \leq 50^{\circ }}$) ${\displaystyle +1.234-2.573\times 10^{-2}\alpha +3.445\times 10^{-4}\alpha ^{2}}$ (para ${\displaystyle 50^{\circ }<\alpha \leq 120^{\circ }}$)
Júpiter	−9.395	${\displaystyle -3.7\times 10^{-4}\alpha +6.16\times 10^{-4}\alpha ^{2}}$ (para ${\displaystyle \alpha \leq 12^{\circ }}$) ${\displaystyle -0.033-2.5\log _{10}{\left(1-1.507\left({\frac {\alpha }{180^{\circ }}}\right)-0.363\left({\frac {\alpha }{180^{\circ }}}\right)^{2}-0.062\left({\frac {\alpha }{180^{\circ }}}\right)^{3}+2.809\left({\frac {\alpha }{180^{\circ }}}\right)^{4}-1.876\left({\frac {\alpha }{180^{\circ }}}\right)^{5}\right)}}$ (para ${\displaystyle \alpha >12^{\circ }}$)
Saturno	−8.914	${\displaystyle -1.825\sin {\left(\beta \right)}+2.6\times 10^{-2}\alpha -0.378\sin {\left(\beta \right)}e^{-2.25\alpha }}$ (para planeta e anéis, ${\displaystyle \alpha <6.5^{\circ }}$ e ${\displaystyle \beta <27^{\circ }}$) ${\displaystyle -0.036-3.7\times 10^{-4}\alpha +6.16\times 10^{-4}\alpha ^{2}}$ (somente para o globo, ${\displaystyle \alpha \leq 6^{\circ }}$) ${\displaystyle +0.026+2.446\times 10^{-4}\alpha +2.672\times 10^{-4}\alpha ^{2}-1.505\times 10^{-6}\alpha ^{3}+4.767\times 10^{-9}\alpha ^{4}}$ (somente para o globo, ${\displaystyle 6^{\circ }<\alpha <150^{\circ }}$)
Urano	−7.110	${\displaystyle -8.4\times 10^{-4}\phi '+6.587\times 10^{-3}\alpha +1.045\times 10^{-4}\alpha ^{2}}$ (para ${\displaystyle \alpha <3.1^{\circ }}$)
Netuno	−7.00	${\displaystyle +7.944\times 10^{-3}\alpha +9.617\times 10^{-5}\alpha ^{2}}$ (para ${\displaystyle \alpha <133^{\circ }}$ e ${\displaystyle t>2000.0}$)

Aqui ${\displaystyle \beta }$ é a inclinação efetiva dos anéis de Saturno (sua inclinação em relação ao observador), que visto da Terra varia entre 0° e 27° ao longo de uma órbita de Saturno, e ${\displaystyle \phi '}$ é um pequeno termo de correção dependendo das latitudes subterrestres e subsolares de Urano. ${\displaystyle t}$ é o ano da Era Comum. A magnitude absoluta de Netuno está mudando lentamente devido aos efeitos sazonais à medida que o planeta se move ao longo de sua órbita de 165 anos ao redor do Sol, e a aproximação acima só é válida após o ano 2000. Para algumas circunstâncias, como ${\displaystyle \alpha \geq 179^{\circ }}$ para Vênus, nenhuma observação está disponível e a curva de fase é desconhecida nesses casos. A fórmula para a Lua só se aplica ao lado mais próximo da Lua, a porção que é visível da Terra.

Exemplo 1: em 1 de janeiro de 2019, Vênus estava ${\displaystyle d_{BS}=0.719{\text{ UA}}}$ do Sol e ${\displaystyle d_{BO}=0.645{\text{ UA}}}$ da Terra, em um ângulo de fase de ${\displaystyle \alpha =93.0^{\circ }}$ (quase um quarto de fase). Sob condições de fase completa, Vênus teria sido visível em ${\displaystyle m=-4.384+5\log _{10}{\left(0.719\cdot 0.645\right)}=-6.09.}$ Contabilizando o ângulo de fase alto, o termo de correção acima produz uma magnitude aparente real de ${\displaystyle m=-6.09+\left(-1.044\times 10^{-3}\cdot 93.0+3.687\times 10^{-4}\cdot 93.0^{2}-2.814\times 10^{-6}\cdot 93.0^{3}+8.938\times 10^{-9}\cdot 93.0^{4}\right)=-4.59.}$ Isso é próximo ao valor de ${\displaystyle m=-4.62}$ previsto pelo Laboratório de Propulsão a Jato (JPL).^[22]

Exemplo 2: Na fase do quarto crescente, a aproximação da Lua dá ${\textstyle -2.5\log _{10}{q(90^{\circ })}=2.71.}$ Com isso, a magnitude aparente da Lua é ${\textstyle m=+0.28+5\log _{10}{\left(1\cdot 0.00257\right)}+2.71=-9.96,}$ próximo ao valor esperado de cerca de ${\displaystyle -10.0}$. No quarto minguante, a Lua é cerca de 0.06 de magnitude mais fraca do que no quarto crescente, porque essa parte de sua superfície tem um albedo menor.

O albedo da Terra varia por um fator de 6, de 0.12 no caso sem nuvens a 0.76 no caso da nuvem altostratus. A magnitude absoluta na tabela corresponde a um albedo de 0.434. Devido à variabilidade do clima, a magnitude aparente da Terra não pode ser prevista com tanta precisão quanto a da maioria dos outros planetas.^[20]

Asteroides

Se um objeto tem uma atmosfera, ele reflete a luz mais ou menos isotropicamente em todas as direções, e seu brilho pode ser modelado como um refletor difuso. Corpos sem atmosfera, como asteroides ou satélites naturais, tendem a refletir a luz mais fortemente na direção da luz incidente, e seu brilho aumenta rapidamente conforme o ângulo de fase se aproxima ${\displaystyle 0^{\circ }}$. Esse brilho rápido perto da oposição é chamado de efeito de oposição. Sua força depende das propriedades físicas da superfície do corpo e, portanto, difere de asteroide para asteroide.^[13]

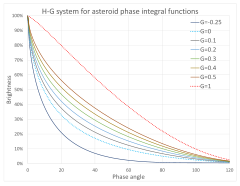
Em 1985, a União Astronômica Internacional (IAU) adotou o sistema semi-empírico ${\displaystyle HG}$, baseado em dois parâmetros ${\displaystyle H}$ e ${\displaystyle G}$ chamados magnitude absoluta e inclinação, para modelar o efeito de oposição para as efemérides publicado pelo Minor Planet Center.^[23]

onde

• a integral de fase é ${\displaystyle q(\alpha )=\left(1-G\right)\phi _{1}\left(\alpha \right)+G\phi _{2}\left(\alpha \right)}$ e
• ${\textstyle \phi _{i}\left(\alpha \right)=\exp {\left(-A_{i}\left(\tan {\frac {\alpha }{2}}\right)^{B_{i}}\right)}}$ para ${\displaystyle i=1}$ ou ${\displaystyle 2}$, ${\displaystyle A_{1}=3.332}$, ${\displaystyle A_{2}=1.862}$, ${\displaystyle B_{1}=0.631}$ e ${\displaystyle B_{2}=1.218}$.^[24]

Esta relação é válida para ângulos de fase ${\displaystyle \alpha <120^{\circ }}$, e funciona melhor quando ${\displaystyle \alpha <20^{\circ }}$.^[25]

O parâmetro de inclinação ${\displaystyle G}$ relaciona-se com o aumento do brilho, normalmente 0.3 mag, quando o objeto está próximo da oposição. É conhecido com precisão apenas para um pequeno número de asteroides, portanto, para a maioria dos asteroides, um valor de ${\displaystyle G=0.15}$ é assumido..^[25] Em casos raros, ${\displaystyle G}$ pode ser negativo.^[24][26] Um exemplo é 101955 Bennu, com ${\displaystyle G=-0.08}$^[27]

Em 2012, o sistema ${\displaystyle HG}$ foi oficialmente substituído por um sistema aprimorado com três parâmetros ${\displaystyle H}$, ${\displaystyle G_{1}}$ e ${\displaystyle G_{2}}$, que produz resultados mais satisfatórios se o efeito de oposição for muito pequeno ou restrito a ângulos de fase muito pequenos. No entanto, a partir de 2022, este sistema ${\displaystyle HG_{1}G_{2}}$ não foi adotado pelo Minor Planet Center nem pelo Laboratório de Propulsão a Jato (JPL).^[13][28]

A magnitude aparente dos asteroides varia conforme eles giram, em escalas de tempo de segundos a semanas, dependendo do período de rotação, até ${\displaystyle 2{\text{ mag}}}$ ou mais.^[29] Além disso, sua magnitude absoluta pode variar com a direção de visualização, dependendo de sua inclinação axial. Em muitos casos, nem o período de rotação nem a inclinação axial são conhecidos, limitando a previsibilidade. Os modelos aqui apresentados não capturam esses efeitos.^[13][25]

Magnitudes cometárias

O brilho dos cometas é dado separadamente como magnitude total (${\displaystyle m_{1}}$, o brilho integrado em toda a extensão visível do coma) e magnitude nuclear (${\displaystyle m_{2}}$, o brilho da região do núcleo sozinho).^[30] Ambas são escalas diferentes da escala de magnitude usada para planetas e asteroides, e não podem ser usadas para uma comparação de tamanho com a magnitude absoluta H de um asteroide.

A atividade dos cometas varia com sua distância do Sol. Seu brilho pode ser aproximado como

onde ${\displaystyle m_{1,2}}$ são as magnitudes aparentes total e nuclear do cometa, respectivamente, ${\displaystyle M_{1,2}}$ são suas magnitudes totais e nucleares "absolutas", ${\displaystyle d_{BS}}$ e ${\displaystyle d_{BO}}$ são as distâncias corpo-sol e corpo-observador, ${\displaystyle d_{0}}$ é a unidade astronômica e ${\displaystyle K_{1,2}}$ são os parâmetros de inclinação que caracterizam a atividade do cometa. Para ${\displaystyle K=2}$, isso se reduz à fórmula para um corpo puramente refletor (não mostrando nenhuma atividade cometária).^[31]

Por exemplo, a curva de luz do cometa C/2011 L4 (PANSTARRS) pode ser aproximada por ${\displaystyle M_{1}=5.41{\text{, }}K_{1}=3.69.}$.^[32] No dia de sua passagem pelo periélio, 10 de março de 2013, o cometa PANSTARRS estava a ${\displaystyle 0.302{\text{ UA}}}$ do Sol e ${\displaystyle 1.109{\text{ UA}}}$ da Terra. Prevê-se que a magnitude aparente total ${\displaystyle m_{1}}$ tenha sido ${\displaystyle m_{1}=5.41+2.5\cdot 3.69\cdot \log _{10}{\left(0.302\right)}+5\log _{10}{\left(1.109\right)}=+0.8}$ naquele momento. O Minor Planet Center dá um valor próximo disso, ${\displaystyle m_{1}=+0.5}$^[33]

Magnitudes absolutas e tamanhos de núcleos de cometas

Cometa	Magnitude absoluta ${\displaystyle M_{1}}$[34]	Núcleo diâmetro
Cometa Sarabat	−3.0	≈100 km?
Cometa Hale-Bopp	−1.3	60 ± 20 km
Cometa Halley	4.0	14.9 x 8.2 km
Novo cometa médio	6.5	≈2 km[35]
C/2014 UN271 (Bernardinelli-Bernstein)	6.7[36]	60–200 km?[37][38]
289P/Blanpain (durante a explosão de 1819)	8.5[39]	320 m[40]
289P/Blanpain (atividade normal)	22.9[41]	320 m

A magnitude absoluta de qualquer cometa pode variar drasticamente. Pode mudar à medida que o cometa se torna mais ou menos ativo ao longo do tempo ou se sofre uma explosão. Isso torna difícil usar a magnitude absoluta para uma estimativa de tamanho. Quando o cometa 289P/Blanpain foi descoberto em 1819, sua magnitude absoluta foi estimada como ${\displaystyle M_{1}=8.5}$.^[39] Foi posteriormente perdido e só foi redescoberto em 2003. Naquela época, sua magnitude absoluta havia diminuído para ${\displaystyle M_{1}=22.9}$,^[41] e percebeu-se que a aparição de 1819 coincidiu com uma explosão. O 289P/Blanpain atingiu o brilho a olho nu (5-8 mag) em 1819, embora seja o cometa com o menor núcleo já caracterizado fisicamente e geralmente não se torna mais brilhante do que 18 mag.^[39][40]

Para alguns cometas que foram observados em distâncias heliocêntricas grandes o suficiente para distinguir entre a luz refletida da coma e a luz do próprio núcleo, uma magnitude absoluta análoga à usada para asteroides foi calculada, permitindo estimar os tamanhos de seus núcleos.^[42]

Meteoros

Para um meteoro, a distância padrão para medição de magnitudes é a uma altitude de 100 km no zênite do observador.^[43][44]

Ver também

• Projeto Araucaria
• Diagrama de Hertzsprung-Russell – relaciona magnitude absoluta ou luminosidade versus cor espectral ou temperatura da superfície.
• Jansky unidade preferida do radioastrônomo – linear na área de potência/unidade
• Lista das estrelas mais luminosas
• Magnitude fotográfica
• Brilho superficial – a magnitude para objetos estendidos
• Ponto zero (fotometria) – o ponto de calibração típico para fluxo estelar

Referências

Ligações externas

• Reference zero-magnitude fluxes Arquivado em 2003-02-22 no Wayback Machine
• International Astronomical Union
• Absolute Magnitude of a Star calculator
• The Magnitude system
• About stellar magnitudes
• Obtain the magnitude of any star – SIMBAD
• Converting magnitude of minor planets to diameter
• Another table for converting asteroid magnitude to estimated diameter