Rozwinięcie multipolowe

Rozwinięcie multipolowe – przedstawienie pola fizycznego, pochodzącego od źródeł zawartych w ograniczonym obszarze, w postaci szeregu potęg odwrotności odległości od punktu, w którym należy znaleźć potencjał. Taki opis jest często wykorzystywany dla potencjałów pól elektromagnetycznych^[1] i grawitacyjnych. Jako że ${\displaystyle m}$-ty wyraz rozwinięcia zanika z odległością od źródeł jak ${\displaystyle {\frac {1}{r^{m}}},}$ to dla wystarczająco dużego ${\displaystyle r}$ dominuje najniższy nieznikający wyraz rozwinięcia. Pierwszy wyraz rozwinięcia ${\displaystyle (m=1)}$ jest członem monopolowym, następny ${\displaystyle (m=2)}$ jest członem dipolowym, trzeci ${\displaystyle (m=3)}$ kwadrupolowym itd. W przypadku rozwinięcia we współrzędnych sferycznych, kolejne wyrazy opisują elementy geometrii pola o coraz mniejszej rozciągłości kątowej. Wyraz monopolowy ma symetrię sferyczną (nie zależy od współrzędnych kątowych), wyraz dipolowy zmienia znak na sferze przy przekraczaniu płaszczyzny symetrii pola.

Sformułowanie matematyczne

Przykład – pole elektrostatyczne

Ograniczony obszar ${\displaystyle \Omega }$ zawiera źródła pola – w elektrostatyce są to ładunki elektryczne – o gęstości ${\displaystyle \varrho =\varrho ({\vec {x'}}).}$ Potencjał pola elektrostatycznego w punkcie opisanym wektorem ${\displaystyle {\vec {x}},}$ odległym od obszaru ${\displaystyle \Omega }$ zawierającego źródła pola można wyrazić za pomocą szeregu Taylora:

${\displaystyle \phi ({\vec {x}})={\frac {1}{4\pi \varepsilon }}\iiint \limits _{\Omega }{\frac {\varrho ({\vec {x'}})}{|{\vec {x}}-{\vec {x'}}|}}d\omega '=\sum \limits _{n=0}^{\infty }\phi _{n}({\vec {x}}),}$

gdzie ${\displaystyle \varepsilon }$ to przenikalność elektryczna, a wyrazy sumy, nazywane potencjałami multipolowymi wyrażają się przez:

${\displaystyle \phi _{n}({\vec {x}})={\frac {(-1)^{n}}{n!}}{\frac {1}{4\pi \varepsilon }}{\frac {\partial ^{n}r_{0}^{-1}}{\partial x^{i_{1}}\ldots \partial x^{i_{n}}}}\iiint \limits _{\Omega }\varrho ({\vec {x'}})x'^{i_{1}}\ldots x'^{i_{n}}d\omega '=(-1)^{n}{\frac {1}{4\pi \varepsilon }}M^{i_{1}\dots i_{n}}{\frac {\partial ^{n}r_{0}^{-1}}{\partial x^{i_{1}}\ldots \partial x^{i_{n}}}}.}$

Symbole ${\displaystyle x^{i}}$ oraz ${\displaystyle x'^{i}}$ oznaczają współrzędne kartezjańskie odpowiednich wektorów, a ${\displaystyle r_{0}}$ jest długością wektora ${\displaystyle {\vec {x}}.}$ Niezależne od ${\displaystyle {\vec {x}}}$ wielkości określone wzorem:

${\displaystyle M^{i_{1}\dots i_{n}}={\frac {1}{n!}}\iiint \limits _{\Omega }\varrho ({\vec {x'}})x'^{i_{1}}\ldots x'^{i_{n}}d\omega '}$

nazywane są momentami multipolowymi rzędu ${\displaystyle n;}$ przykładowo moment multipolowy rzędu 1 nazywa się momentem dipolowym. W elektrostatyce potencjały multipolowe można interpretować jako potencjały pochodzące od szczególnych układów ładunków punktowych.

Wyrażenie przez harmoniki sferyczne

Potencjał ${\displaystyle V}$ pola w punkcie opisanym współrzędnymi sferycznymi ${\displaystyle (r,\theta ,\phi ),}$ odległym od ograniczonego obszaru, zawierającego źródła pola, można wyrazić za pomocą sumy harmonik sferycznych mnożonych przez współczynniki ${\displaystyle C_{l,j}^{m}}$ zależne od promienia ${\displaystyle r{:}}$

${\displaystyle V(r,\theta ,\phi )=\sum _{l=0}^{\infty }\,\sum _{m=-l}^{l}\,C_{l}^{m}(r)\,Y_{l}^{m}(\theta ,\phi )=\sum _{j=1}^{\infty }\,\sum _{l=0}^{\infty }\,\sum _{m=-l}^{l}\,{\frac {D_{l,j}^{m}}{r^{j}}}\,Y_{l}^{m}(\theta ,\phi ),}$

gdzie ${\displaystyle D_{l,j}^{m}}$ to stałe współczynniki.

Monopol

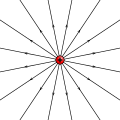
Pole monopola jest sferycznie symetryczne. Taki charakter ma np. pole elektryczne pojedynczego ładunku elektrycznego lub pole grawitacyjne wytwarzane przez punkt materialny. W elektrostatyce moment monopolowy jest równy całkowitemu ładunkowi układu:

${\displaystyle M^{0}=\iiint \limits _{\Omega }\varrho ({\vec {x'}})d\omega '=Q.}$

Prawo Gaussa dla magnetyzmu wyraża założenie, że pole magnetyczne nie ma źródeł, tj. nie istnieją monopole magnetyczne, oddzielne bieguny „północny” i „południowy”. Takie cząstki nigdy nie zostały zaobserwowane, chociaż pojawiają się w niektórych teoriach fizycznych (teoriach wielkiej unifikacji).

Dipol

 Osobny artykuł: dipol.

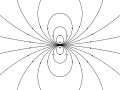
Pole dipolowe ma symetrię osiową. Najprostsze pole magnetyczne, np. wytwarzane przez małą, symetryczną pętlę z prądem, ma charakter dipolowy. Ziemskie pole magnetyczne generalnie ma charakter dipolowy (oprócz okresów przebiegunowania Ziemi), ale występujące lokalnie anomalie magnetyczne wskazują, że wyższe składowe pola też nie są zerowe.

Elektryczny moment dipolowy ma składowe określone wzorem:

${\displaystyle M^{i}=\iiint \limits _{\Omega }\varrho ({\vec {x'}})x'^{i}d\omega ',}$

zatem w przypadku układu ${\displaystyle N}$ ładunków punktowych wyraża się wzorem:

${\displaystyle {\vec {M}}=\sum _{i=1}^{N}q_{i}{\vec {x_{i}}}.}$

Kwadrupol

 Osobny artykuł: kwadrupol.

Pole kwadrupola jest symetryczne względem płaszczyzny, w której znajdują się źródła pola. Przykładem kwadrupola jest układ cewek wykorzystywany jako analizator masy, oraz do kolimacji wiązek cząstek naładowanych.

Moment kwadrupolowy rozkładu ładunków elektrycznych wyraża się wzorem:

${\displaystyle M^{i_{1}i_{2}}={\frac {1}{2}}\iiint \limits _{\Omega }\varrho ({\vec {x'}})x'^{i_{1}}x'^{i_{2}}d\omega ',}$

wielkość ta jest tensorem symetrycznym.

Przypisy

Bibliografia

• David J. Griffiths: Podstawy elektrodynamiki. Warszawa: Wydawnictwo Naukowe PWN, 2001. ISBN 83-01-13376-7.brak strony w książce
• Roman S. Ingarden, Andrzej Jamiołkowski: Elektrodynamika klasyczna. Warszawa: PWN, 1980. ISBN 83-01-00454-9.brak strony w książce