Bielliptisk overføringsbane

I romfart er en bielliptisk overføringsbane en mulig bane for et romfartøy mellom to baner rundt det samme sentrale legemet (for eksempel jorden eller solen). I forskjell med Hohmann-banen som går direkte mellom start- og målbanen, skjer overføringen via to transferellipser. Den første går «utover målet», den andre fører til målbanen. Det høres kanskje meningsløst ut, men når målbanen er mye høyere enn startbanen, er den bielliptiske overføringsbanen mindre krevende i energi ^[1]. Derfor ser denne artikkelen bare på tilfellet å gå fra en nedre til en høyere omløpsbane.

Selv om det prinsipielt er mulig å sette banehøyden ned med en bielliptisk overføring, har det ingen fordel framfor en Hohmann-bane. Et unntak er å bremse ved hjelp av atmosfæren, det såkalte «aerobraking» (som ikke er en bielliptisk overføringsbane denne artikkelen handler om).

Denne artikkelen beskriver derfor bare det relevante tilfellet at målbanen er lengre unna fra det sentrale legemet enn startbanen. De andre forenklingene er at omløpsbaner er sirkelformede og i det samme planet, at hastigheten endrer seg umiddelbart og at det er ingen forstyrrelser for eksempel på grunn av andre himmellegemet.

Beregning

Hastighet

Den viktigste ligningen for å beregne koplanare overføringer (som den bielliptiske overføringsbanen) er den såkalte Vis-Viva ligningen ^[1]

${\displaystyle v={\sqrt {\mu \left({\frac {2}{r}}-{\frac {1}{a}}\right)}}}$

• ${\displaystyle r}$ og ${\displaystyle v}$ er den aktuelle avstanden og hastigheten til romfartøyet rundt sentrallegemet
• ${\displaystyle a}$ er den store halvaksen til banen
• ${\displaystyle \mu =GM}$ er gravitasjonsparameteren til sentrallegemet (massen ${\displaystyle M}$ multiplisert med gravitasjonskonstanten ${\displaystyle G}$)

For en sirkelformede bane (${\displaystyle r=a}$) forenkler seg ligningnen slik

${\displaystyle v={\sqrt {\frac {\mu }{r}}}}$

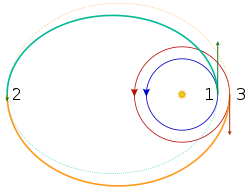
Figuren til høyre viser hvordan den bielliptiske overføringen skjer. Romfartøyet befinner seg på en sireklformede omløpsbane (blå) med radius ${\displaystyle r_{1}}$. Hastigheten er konstant ${\displaystyle v_{1}={\sqrt {\frac {\mu }{r_{1}}}}}$. Målet er å nå den høyrere sireklformede bane (rød) med radius ${\displaystyle r_{2}}$.

1. En øyeblikkelig hastighetsforhøyelse bringer satelliten på den første transferellipsen (cyan) med den store halvaksen ${\displaystyle a_{1}}$. Den første hastighetsendringen er altså \cite{Vallado}
   ${\displaystyle \Delta v_{1}={\sqrt {\mu \left({\frac {2}{r_{1}}}-{\frac {1}{a_{1}}}\right)}}-{\sqrt {\frac {\mu }{r_{1}}}}}$
   Man må gjøre den tangensjal i flyretningen. For startbanen er en sirkel, kan det skje overalt.
2. Når apoapsen er nådd, befinner seg satelliten i avstand ${\displaystyle r_{b}=2a_{1}-r_{1}}$ til sentrallegemet. Nå kommer den andre øyeblikkelige hastighetsforhøyelsen til den andre transferellipsen (oransje) med den store halvaksen ${\displaystyle a_{2}={\tfrac {r_{b}+r_{2}}{2}}}$. Igjen må hastighetsendringen være tangensjal i flyretning. Størrelsen er
   ${\displaystyle \Delta v_{2}={\sqrt {\mu \left({\frac {2}{r_{b}}}-{\frac {1}{a_{2}}}\right)}}-{\sqrt {\mu \left({\frac {2}{r_{b}}}-{\frac {1}{a_{1}}}\right)}}}$
3. Når periapsen til den andre transferellipsen er nådd, kommer den tredje hastighetsendringen. Denne gangen må man bremse satelliten slik at den forblir på den sirkelformede omløpsbanen.
   ${\displaystyle \Delta v_{3}={\sqrt {\frac {\mu }{r_{2}}}}-{\sqrt {\mu \left({\frac {2}{r_{2}}}-{\frac {1}{a_{2}}}\right)}}}$

Til sammen er drivstoffbehovet (Delta v)

${\displaystyle \Delta v=\Delta v_{1}+\Delta v_{2}+\Delta v_{3}=\left({\sqrt {\mu \left({\frac {2}{r_{1}}}-{\frac {1}{a_{1}}}\right)}}-{\sqrt {\frac {\mu }{r_{1}}}}\right)+\left({\sqrt {\mu \left({\frac {2}{r_{b}}}-{\frac {1}{a_{2}}}\right)}}-{\sqrt {\mu \left({\frac {2}{r_{b}}}-{\frac {1}{a_{1}}}\right)}}\right)+\left({\sqrt {\frac {\mu }{r_{2}}}}-{\sqrt {\mu \left({\frac {2}{r_{2}}}-{\frac {1}{a_{2}}}\right)}}\right)}$

Hvis radien til målbanen er mer enn 15,58 gang høyere enn radien til startbanen, trenger hvert bielliptisk overføringsbane mindre drivstoff enn en Hohmann-bane, så lenge ${\displaystyle r_{b}>r_{2}}$ ist. Under denne verdien kan en biellitpisk overføringsbane ha mindre behov for Delta v (se avsnitt #Sammenligning med Hohmann-banen).

Tid

Tiden til overføringen la seg beregne fra de halve omløpstidene til transferellipsene. Omløpstiden ${\displaystyle T}$ er ifølge Keplers tredje lov ^[1]

${\displaystyle T=2\pi {\sqrt {\frac {a^{3}}{\mu }}}}$

Altså er transfertiden til en bielliptisk overføring

${\displaystyle \Delta t=\pi {\sqrt {\frac {a_{1}^{3}}{\mu }}}+\pi {\sqrt {\frac {a_{2}^{3}}{\mu }}}}$

Det er betydelig lengre enn en Hohmann-bane, noe som er en viktig ulempe til den biellitpiske overføringsbanen (se avsnitt #Sammenligning med Hohmann-banen).

Grensetilfellet Hohmann-bane

Hivs ${\displaystyle r_{b}=r_{2}}$ går den bielliptiske overføringsbanen over til Hohmann-banen ^[1].

Grensetilfellet biparabolisk overføringsbane

I grensetilfellet ${\displaystyle r_{b}\rightarrow \infty }$ går den bielliptiske overføringsbanen over til en biparabolisk overføringsbanen ^[1].

Dette tilfellet er ren teoretisk fordi satelliten fjerner seg uendelig langt fra sentrallegemet. I tillegg gjelder forenklingen at det er et tolegemeproblem, ikke lenger. Likevel er det interessant og se på den i hensikt til sammenligningen som kommer i det neste avsnittet.

1. Romfartøyet blir nå brakt på en unnslipningparabel (grønn).
   ${\displaystyle \Delta v_{1}=\left({\sqrt {2}}-1\right){\sqrt {\frac {\mu }{r_{1}}}}}$
2. Når den er uendelig langt unna (${\displaystyle \infty }$) går hastigheten ned til 0. Et infinitesimal lite fremstøt er nok til å bringe satelliten på den andre transferparabelen (oransje).
   ${\displaystyle \Delta v_{2}=0}$
3. På toppunktet til den andrer parabelen må man nå igjen bremse satelliten slik at den forblir på den sirkelformede målbanen.
   ${\displaystyle \Delta v_{3}=\left({\sqrt {2}}-1\right){\sqrt {\frac {\mu }{r_{2}}}}}$

Til sammen er behovet for drivstoff (Delta v)

${\displaystyle \Delta v=\Delta v_{1}+\Delta v_{2}+\Delta v_{3}=\left({\sqrt {2}}-1\right)\left({\sqrt {\frac {\mu }{r_{1}}}}+{\sqrt {\frac {\mu }{r_{2}}}}\right)}$

For alle overføringer der ${\displaystyle r_{2}>11,94\,r_{1}}$, er denne verdien mindre enn for Hohmann-banen. Den biparaboliske overføringsbanen er grensetilfellet til den bielliptiske overføringsbanen som sparer mest Delta v ^[2].

Sammenligning med Hohmann-banen

Hastighet

Figuren til høyre viser behovet for Delta v, et mål for drivstoff og altså energi, når man gjør en overføring mellom en sirkelformede omløpsbane med radius ${\displaystyle r_{1}}$ til en sirkelformede bane med radius ${\displaystyle r_{2}}$.

${\displaystyle \Delta v}$ er normert med ${\displaystyle v_{1}}$, slik at man kan sammenligne generelt. Fire kurver er vist: drivstoffbehovet for en Hohmann-bane (blå), for en bielliptisk overføringsbane med ${\displaystyle \alpha ={\tfrac {r_{b}}{r_{1}}}=20+{\tfrac {r_{2}}{r_{1}}}}$ (rød), for en bielliptisk overføringsbane med ${\displaystyle \alpha ={\tfrac {r_{b}}{r_{1}}}=100+{\tfrac {r_{2}}{r_{1}}}}$ (cyan) og for en biparabolisk overføringsbane (${\displaystyle r_{b}\rightarrow \infty }$) (grønn) ^[3].

Man ser at Hohmann-banen er best i energihensikt så lenge radiusforholdet er mindre enn 11,94. Når den er høyere enn 15,58, er hvert bielliptisk overføringsbane bedre så lenge ${\displaystyle r_{b}>r_{2}}$.

Imellom 11,94 og 15,58 er avstanden til den felles apoapsen til begge transferellipsene (punkt 2 i de figurene om de bielliptiske og biparaboliske overføringsbanene) avgjørende.

Tabellen som folger lister noen tilfeller hvor stor ${\displaystyle \alpha ={\tfrac {r_{b}}{r_{1}}}}$ (avstnaden til apoapsen i forhold til radien til startbanen) må minst være, slik at den bielliptiske overføringsbanen er bedre når det gjelder energibehov.

Minimal ${\displaystyle \alpha ={\tfrac {r_{b}}{r_{1}}}}$, slik at den bielliptiske overføringsbanen krever mindre energi ^[2].

Radiusforholdet ${\displaystyle {\tfrac {r_{2}}{r_{1}}}}$	Minimal ${\displaystyle \alpha ={\tfrac {r_{b}}{r_{1}}}}$	Bemerkninger
0 til 11,94	-	Hohmann-banen er billigere
11,94	${\displaystyle \infty }$	Biparabolisk overføringsbane
12	815,81
13	48,90
14	26,10
15	18,19
15,58	15,58
større enn 15,58	større enn ${\displaystyle {\tfrac {r_{2}}{r_{1}}}}$	Hvert bielliptisk overføringsbanen er billigere

Denne sammenhengen som er ikke nødvendigvis intuitivt, kan man forklare med Oberth Effect.

Tid

Den lange overføringstiden til den bielliptiske overføringen

${\displaystyle \Delta t=\pi {\sqrt {\frac {a_{1}^{3}}{\mu }}}+\pi {\sqrt {\frac {a_{2}^{3}}{\mu }}}}$

er en stor ulempe. I det biparaboliske grensetilfellet blir den til og med uendelig lang.

Tiden til Hohmann-overføringen i sammenligning er med

${\displaystyle \Delta t=\pi {\sqrt {\frac {a^{3}}{\mu }}}}$

mindre enn halvparten fordi man går bare over en transferellipse.

Eksempel

Et eksempel (se Example 6-2 i ^[1]) hjelper å forstå overføringene.

En satellitt som er på bane rundt jorden, skal gå fra en sirkelformede startbane med ${\displaystyle r_{1}=6569\,\mathrm {km} }$ til den sirkelformede målbanen med radius ${\displaystyle r_{2}=382688\,\mathrm {km} }$. Hastigheten og tiden til hohmann-banen, den bielliptiske overføringsbanen og den biparaboliske overføringsbanen blir sammenlignt.

Radiusforholdet er omtrent 58,25. Den bielliptiske overføringsbanen og den biparaboliske overføringsbanen skal altså behøve mindre Delta v en Hohmann-banen. Man må velge en ${\displaystyle r_{b}>r_{2}}$ for den bielliptiske overføringsbanen, i eksemplet er ${\displaystyle r_{b}=100\,r_{1}}$.

Tabellen som folger viser sammenligningen:

	Hohmann	bielliptisk ${\displaystyle \alpha =100}$	biparabolisk
${\displaystyle \Delta v_{1}}$	${\displaystyle 3,133\,\mathrm {\tfrac {km}{s}} }$	${\displaystyle 3,172\,\mathrm {\tfrac {km}{s}} }$	${\displaystyle 3,226\,\mathrm {\tfrac {km}{s}} }$
${\displaystyle \Delta v_{2}}$	${\displaystyle 0,833\,\mathrm {\tfrac {km}{s}} }$	${\displaystyle 0,559\,\mathrm {\tfrac {km}{s}} }$	${\displaystyle 0\,\mathrm {\tfrac {km}{s}} }$
${\displaystyle \Delta v_{3}}$	ingen ${\displaystyle \Delta v_{3}}$	${\displaystyle 0,127\,\mathrm {\tfrac {km}{s}} }$	${\displaystyle 0,423\,\mathrm {\tfrac {km}{s}} }$
${\displaystyle \mathbf {\Delta v} }$ sum	${\displaystyle \mathbf {3,966\,\mathrm {\tfrac {km}{s}} } }$	${\displaystyle \mathbf {3,858\,\mathrm {\tfrac {km}{s}} } }$	${\displaystyle \mathbf {3,649\,\mathrm {\tfrac {km}{s}} } }$
Tid	${\displaystyle 118\,\mathrm {h} }$ ${\displaystyle 40\,\mathrm {min} }$ ${\displaystyle 59\,\mathrm {s} }$	${\displaystyle 782\,\mathrm {h} }$ ${\displaystyle 9\,\mathrm {min} }$ ${\displaystyle 27\,\mathrm {s} }$	${\displaystyle \infty }$

Se også

• A. F. B. A. Prado, Journal of the Brazilian Society of Mechanical Sciences and Engineering, vol. 25,‎ 2003, p. 122–128 (ISSN 1678-5878, DOI 10.1590/S1678-58782003000200003, online)

Referanser