Triangolo isoscele

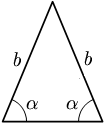
In geometria, si definisce triangolo isoscele un triangolo che possiede due lati congruenti.

Vale il seguente teorema: "Un triangolo è isoscele se e solo se ha due angoli congruenti". Questo teorema costituisce la quinta proposizione del Libro I degli Elementi di Euclide ed è noto come pons asinorum.

In un triangolo isoscele la bisettrice relativa all'angolo al vertice coincide con la mediana, l'altezza e l'asse relativi alla base.

Particolari triangoli isosceli sono i triangoli equilateri e i triangoli rettangoli isosceli. Esistono anche triangoli isosceli acutangoli e ottusangoli.

I triangoli isosceli rettangoli sono tutti simili tra di loro, come i triangoli equilateri.

Simmetrie

Un triangolo isoscele che non sia equilatero è invariante solo per la riflessione rispetto alla bisettrice dell'angolo diverso dai due rimanenti. Il suo gruppo di simmetria, oltre alla trasformazione identità, comprende solo questa riflessione e quindi è isomorfo al gruppo di due elementi, ovvero al gruppo moltiplicativo sull'insieme ${\displaystyle \{1,-1\}}$.

Triangoli isosceli in geometria analitica

Teorema 1: Condizione necessaria e sufficiente affinché un triangolo con la base parallela agli assi sia isoscele è che abbia i due lati di coefficiente angolare opposto.

Dimostrazione.

Date le tre rette

1. ${\displaystyle y=k}$
2. ${\displaystyle y=mx}$
3. ${\displaystyle y=-mx}$

ne calcoliamo l'intersezione.

${\displaystyle \left\{{\begin{array}{rl}&y=k\\&y=mx\end{array}}\right.}$

${\displaystyle \left\{{\begin{array}{rl}&x={\frac {k}{m}}\\&y=k\end{array}}\right.}$

${\displaystyle A\left({\frac {k}{m}},k\right)}$

${\displaystyle \left\{{\begin{array}{rl}&y=k\\&y=-mx\end{array}}\right.}$

${\displaystyle \left\{{\begin{array}{rl}&x=-{\frac {k}{m}}\\&y=k\end{array}}\right.}$

${\displaystyle B\left(-{\frac {k}{m}},k\right)}$

${\displaystyle \left\{{\begin{array}{rl}&y=mx\\&y=-mx\end{array}}\right.}$

${\displaystyle \left\{{\begin{array}{rl}&x=0\\&y=0\end{array}}\right.}$

${\displaystyle {\rm {C}}(0,0)}$

Ora calcoliamo la distanza dei segmenti ${\displaystyle AC}$ e ${\displaystyle BC}$.

${\displaystyle AC={\sqrt {\left({\frac {k}{m}}\right)^{2}+k^{2}}}}$

${\displaystyle BC={\sqrt {\left(-{\frac {k}{m}}\right)^{2}+k^{2}}}}$

Quindi il triangolo è isoscele sulla base ${\displaystyle AB}$. In modo analogo si dimostra il caso della base parallela all'asse ${\displaystyle y}$.

Viceversa costruiamo un triangolo isoscele con la base parallela all'asse delle ascisse.

Dati i due punti:

1. ${\displaystyle {\rm {A}}(x_{1},k)}$
2. ${\displaystyle {\rm {B}}(x_{2},k)}$

poiché il vertice di un triangolo isoscele giace sulla stessa retta del punto medio della base, prima troviamo ${\displaystyle M}$ e poi ${\displaystyle C}$.

${\displaystyle M\left({\frac {x_{1}+x_{2}}{2}},k\right)}$

Quindi troviamo ${\displaystyle C}$, che avrà la stessa ascissa di ${\displaystyle M}$ e diversa ordinata.

${\displaystyle C\left({\frac {x_{1}+x_{2}}{2}},h\right)}$

Verifichiamo che il triangolo è isoscele:

${\displaystyle AC={\sqrt {\left({\frac {x_{1}-x_{2}}{2}}\right)^{2}+(k-h)^{2}}}}$

${\displaystyle BC={\sqrt {\left({\frac {x_{2}-x_{1}}{2}}\right)^{2}+(k-h)^{2}}}}$

Ora calcoliamo il coefficiente angolare dei due lati:

${\displaystyle mAC=(h-k)\cdot \left({\frac {2}{x_{2}-x_{1}}}\right)={\frac {2(h-k)}{x_{2}-x_{1}}}}$

${\displaystyle mBC=(h-k)\cdot \left({\frac {2}{x_{1}-x_{2}}}\right)={\frac {2(h-k)}{x_{1}-x_{2}}}}$

Teorema 2: Condizione necessaria e sufficiente affinché un triangolo con la base parallela alla bisettrice di due quadranti sia isoscele è che abbia i due lati di coefficiente angolare inverso.

Dimostrazione.

Date le tre rette

1. ${\displaystyle y=x+q}$
2. ${\displaystyle y=mx}$
3. ${\displaystyle y={\frac {1}{m}}x}$

ne calcoliamo l'intersezione.

${\displaystyle \left\{{\begin{array}{rl}&y=x+q\\&y=mx\end{array}}\right.}$

${\displaystyle \left\{{\begin{array}{rl}&x(m-1)=q\\&y=mx\end{array}}\right.}$

${\displaystyle \left\{{\begin{array}{rl}&x={\frac {q}{m-1}}\\&y={\frac {mq}{m-1}}\end{array}}\right.}$

${\displaystyle A\left({\frac {q}{m-1}},{\frac {mq}{m-1}}\right)}$

${\displaystyle \left\{{\begin{array}{rl}&y=x+q\\&y={\frac {1}{m}}x\end{array}}\right.}$

${\displaystyle \left\{{\begin{array}{rl}&x(1-m)=mq\\&y={\frac {1}{m}}x\end{array}}\right.}$

${\displaystyle \left\{{\begin{array}{rl}&x={\frac {mq}{1-m}}\\&y={\frac {q}{1-m}}\end{array}}\right.}$

${\displaystyle B\left({\frac {mq}{1-m}},{\frac {q}{1-m}}\right)}$

${\displaystyle \left\{{\begin{array}{rl}&y={\frac {1}{m}}x\end{array}}\right.}$

${\displaystyle \left\{{\begin{array}{rl}&x=0\\&y=0\end{array}}\right.}$

${\displaystyle {\rm {C}}(0,0)}$

Ora calcoliamo la distanza dei segmenti ${\displaystyle AC}$ e ${\displaystyle BC}$.

${\displaystyle AC={\sqrt {\left({\frac {q}{m-1}}\right)^{2}+\left({\frac {mq}{m-1}}\right)^{2}}}}$

${\displaystyle BC={\sqrt {\left({\frac {mq}{1-m}}\right)^{2}+\left({\frac {q}{1-m}}\right)^{2}}}}$

Quindi il triangolo è isoscele sulla base ${\displaystyle AB}$. In modo analogo si dimostra il caso della base parallela all'asse ${\displaystyle y}$.

Viceversa costruiamo un triangolo isoscele con la base parallela alla bisettrice del primo e terzo quadrante (lo stesso vale per quella parallela alla bisettrice del secondo e quarto quadrante).

Dati i due punti:

1. ${\displaystyle {\rm {A}}(0,q)}$
2. ${\displaystyle {\rm {B}}(-q,0)}$

poiché il vertice di un triangolo isoscele giace sulla stessa retta del punto medio della base, prima troviamo ${\displaystyle M}$ e poi ${\displaystyle C}$.

${\displaystyle M\left(-{\frac {q}{2}},{\frac {q}{2}}\right)}$

Quindi troviamo ${\displaystyle C}$, che si trova sulla retta di equazione ${\displaystyle y=-x}$ perpendicolare alla base e passante per ${\displaystyle M}$.

${\displaystyle C(h,-h)}$

dove ${\displaystyle h}$ è un numero reale arbitrario diverso da ${\displaystyle 0}$.

Verifichiamo che il triangolo è isoscele:

${\displaystyle AC={\sqrt {h^{2}+(q+h)^{2}}}}$

${\displaystyle BC={\sqrt {(-q-h)^{2}+h^{2}}}}$

Ora calcoliamo il coefficiente angolare dei due lati:

${\displaystyle mAC={\frac {-h-q}{h}}=-{\frac {h+q}{h}}}$

${\displaystyle mBC={\frac {-h}{h+q}}=-{\frac {h}{h+q}}}$

Voci correlate

• Triangolo
• Triangolo equilatero
• Triangolo aureo
• Triangolo scaleno
• Teorema diretto dei triangoli isosceli

Altri progetti

• Wikimedia Commons contiene immagini o altri file su triangolo isoscele

Collegamenti esterni

• triangolo isoscele, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) Eric W. Weisstein, Triangolo isoscele, su MathWorld, Wolfram Research.

V · D · M Poligoni
Poligoni per numero di lati	Triangolo (3) · Quadrilatero (4) · Pentagono (5) · Esagono (6) · Ettagono (7) · Ottagono (8) · Ennagono (9) · Decagono (10) · Endecagono (11) · Dodecagono (12) · Tridecagono (13) · Tetradecagono (14) · Pentadecagono (15) · Esadecagono (16) · Eptadecagono (17) · Ottadecagono (18) · Ennadecagono (19) · Icosagono (20) · Endeicosagono (21) · Doicosagono (22) · Triacontagono (30) · Pentacontagono (50) · 257-gono (257) · Chiliagono (1 000) · Miriagono (10 000) · 65537-gono (65 537)
Triangoli	In base ai lati: Triangolo equilatero · Triangolo isoscele · Triangolo scaleno · In base agli angoli: Triangolo rettangolo · Triangolo acutangolo · Triangolo ottusangolo
Quadrilateri	Quadrato · Rettangolo · Parallelogramma · Rombo · Trapezio · Aquilone
Poligoni stellati	Pentagramma · Esagramma · Eptagramma · Ottagramma · Enneagramma · Decagramma · Endecagramma · Dodecagramma
Altri	Poligono regolare · Poligono equilatero · Poligono equiangolo · Poligono sghembo