Triangolo aureo

In geometria l'aggettivo aureo potrebbe riferirsi a un qualsiasi triangolo avente una proporzionalità aurea tra due dei suoi elementi, cioè un rapporto uguale al famoso numero aureo ≈ 1,618. Di fatto però tra i tanti possibili triangoli con questa caratteristica normalmente in letteratura ci si riferisce ai due triangoli isosceli ricavabili dal pentagono, quello acutangolo (36°, 72° e 72°) e quello ottusangolo (108°, 36° e 36°) che hanno entrambi i lati diversi in rapporto aureo. Molto spesso il nome triangolo aureo è riservato al primo mentre il secondo è chiamato gnomone aureo. Questa nomenclatura è però stata criticata[1] per non essere caratterizzante in quanto le due figure sono entrambe triangoli aurei ed entrambe gnomoni l'una dell'altra e anche perché non sembra esistere alcun motivo oggettivo per privilegiare uno dei due. Alcuni autori preferiscono distinguere i due triangoli chiamandoli aureo di primo tipo e aureo di secondo tipo[2][3] ma anche questa scelta li differenzia solo convenzionalmente. È stato perciò proposto di chiamare i due aurei acutaureo e ottusaureo evidenziando la loro effettiva differenza geometrica[1]
Triangolo aureo (acutaureo)
Questo triangolo è un triangolo isoscele avente i due lati uguali in rapporto aureo con il terzo lato, φ:1 (1,618:1) e angoli di 36°, 72° e 72°. Viene utilizzato per dimostrare che la diagonale del pentagono è in rapporto aureo col lato, e con l'aggiunta di altri due "ottusaurei", detti anche gnomoni aurei, ne completa la figura
Costruzione

Vi sono molti modi per costruire geometricamente un triangolo aureo, diversi di questi passano per la costruzione del pentagono regolare, ma sono piuttosto scomodi per via dell'oggettiva maggiore complicatezza che richiede la costruzione preliminare del pentagono stesso.
I sistemi più diretti e semplici si basano su procedimenti derivati dalla costruzione del rettangolo aureo e proprio in esso trovano la giustificazione algebrica. Per costruire un triangolo aureo su un segmento dato AB, si può procedere nel seguente modo:
- Tracciare una perpendicolare passante per uno dei due estremi, in questo caso A, e riportarvi il punto C a una distanza pari alla metà di AB;
- Con centro in C, si riporta la distanza da questo all'altro estremo del segmento, CB, individuando il punto D;
- Con centro in A si riporta la lunghezza totale trovata, AD, sulla mediana del segmento o la si fa incrociare con l'omologa dall'estremo opposto, designando il terzo punto della terna triangolare.
La spiegazione è rapida; innanzitutto si tratta di trovare un lato che sia in rapporto aureo con la base data e si riporta una metà di questa ½, a cui si aggiunge l'ipotenusa del triangolo CAB, calcolabile per mezzo del teorema di Pitagora:
Ovviamente il rettangolo ABDD'è il rettangolo aureo.
Particolarità geometriche

Il triangolo aureo ha molte proprietà in comune con quelle che sono più note come attribuite al rettangolo aureo. Per la sua caratteristica di avere gli angoli alla base di ampiezza doppia (72°) rispetto all'angolo al vertice (36°), è possibile, bisecando uno di questi, ricavare una successione infinita di triangoli aurei minori. Contestualmente alla successione di triangoli omologhi, viene anche prodotta una successione di gnomoni aurei di completamento, grazie ai quali è possibile tracciare una "spirale di Fibonacci", ovvero una spirale che approssima la spirale aurea autentica, tracciando in contiguità una successione archi di 108° di ampiezza, ovvero l'angolo al vertice dello gnomone.
La "spirale di Fibonacci" in questione,[4], come la spirale aurea vera, non ha mai fine, ma si "arrotola" attorno ad un punto asintotico, un sito all'incontro della mediana degli angoli alla base opposti rispetto a quello verso cui punta il primo triangolo che possiamo trovare nella serie. Anche in questo punto si può registrare un parallelismo col rettangolo aureo, dove il punto asintotico si registra invece all'incrocio delle diagonali della successione di rettangoli.
Negli altri poligoni
In relazione ad altri poligoni il triangolo aureo può essere segnalato nel:
Decagono
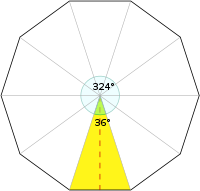
Pentagono

Pentagramma

Nel decagono il triangolo aureo appare come uno spicchio di torta pari a un decimo della sua area, questo è possibile perché il vertice del triangolo è esattamente di 36° cioè un decimo esatto dell'angolo giro. Inoltre questo permette di sapere con esattezza il suo apotema, coincidente all'altezza del triangolo, pari a:
Nel pentagono regolare è inscrivibile un triangolo aureo cui i lati obliqui corrispondono alle diagonali e la base al lato; il resto della figura viene completata da altri due triangoli, anch'essi isosceli e di proporzioni auree ma invertite nelle parti, detti gnomoni aurei proprio perché figure di completamento del pentagono.
Nel pentagramma, cioè una stella a 5 punte, invece il triangolo aureo si trova in quelle che rappresentano le punte della stella. Anche in questo caso tutto dipende dai legami del triangolo con il pentagono, il pentagramma infatti è ottenibile prolungando i lati del pentagono regolare che formano degli angoli esterni di 72°[5], la stessa ampiezza degli angoli alla base del triangolo aureo.
Reciprocità gnomonica
Le proprietà dell'acutaureo trovano corrispondenza in quelle dell'ottusaureo. Se è vero che quest'ultimo è lo gnomone del primo è anche vero il viceversa. Se è vero che l'acutaureo individua una spirale logaritmica simile a quella del rettangolo aureo, lo stesso si può dire dell'ottusaureo[6] e anche dei poligoni mostrati[7][8] che potrebbero essi stessi definirsi aurei in quanto pari all'accumulo di una serie geometrica infinita di triangoli aurei:[1]
-
 L' ottusaureo nel ruolo di gnomone dell'acutaureo
L' ottusaureo nel ruolo di gnomone dell'acutaureo -
 L'acutaureo nel ruolo di gnomone dell'ottusaureo
L'acutaureo nel ruolo di gnomone dell'ottusaureo -
 L'ottusaureo nel ruolo di gnomone di un ennagono
L'ottusaureo nel ruolo di gnomone di un ennagono -
 L'acutaureo nel ruolo di gnomone di un ottagono
L'acutaureo nel ruolo di gnomone di un ottagono -
 La coppia di triangoli aurei isosceli nel ruolo di gnomone di un pentagono
La coppia di triangoli aurei isosceli nel ruolo di gnomone di un pentagono -
 La coppia di aurei disegna infiniti pentagoni regolari e pentagrammi
La coppia di aurei disegna infiniti pentagoni regolari e pentagrammi
Coppie di triangoli aurei tassellanti
Anche la varietà infinita aperiodica delle tassellature di Penrose conferma che è in coppia che i due triangoli aurei danno il meglio di sé. I due rombi di Penrose e l'altra coppia tassellante costituita da dardo e aquilone si possono infatti ottenere raddoppiando triangoli aurei isosceli.[1]
-
 Rombo spesso: unione per il lato maggiore di due triangoli aurei isosceli ottusangoli
Rombo spesso: unione per il lato maggiore di due triangoli aurei isosceli ottusangoli -
 Rombo sottile: unione per il lato minore di due triangoli aurei isosceli acutangoli
Rombo sottile: unione per il lato minore di due triangoli aurei isosceli acutangoli -
![Rombi di Penrose[9]](//upload.wikimedia.org/wikipedia/commons/thumb/c/cf/Duerombi.gif/120px-Duerombi.gif) Rombi di Penrose[9]
Rombi di Penrose[9] -
 Dardo: unione per il lato minore di due triangoli aurei isosceli ottusangoli
Dardo: unione per il lato minore di due triangoli aurei isosceli ottusangoli -
 Aquilone: unione per il lato maggiore due triangoli aurei isosceli acutangoli
Aquilone: unione per il lato maggiore due triangoli aurei isosceli acutangoli -
![Dardi e aquiloni[10]](//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/DardoAquilone.gif/120px-DardoAquilone.gif) Dardi e aquiloni[10]
Dardi e aquiloni[10]
Note
- ^ a b c d Giorgio Pietrocola, triangoli aurei, in Gnomoni aurei e no, Archimede, Le Monnier, gennaio/marzo 2022, pp. 3-10, ISSN 0390-5543 (WC · ACNP).
- ^ Roberto Bigoni, Triangoli aurei, decagoni e pentagoni., su Numero aureo, robertobigoni.it.
- ^ Antonio De Lisa, Triangoli aurei di due tipi, su La sezione aurea, filosofiacomparata.org, 2013.
- ^ Solitamente si parla di "spirale di Fibonacci" limitatamente al caso del rettangolo aureo, le spirali ricavate, infatti, in tutte e due i casi, sono differenti, basti considerare la prima è il risultato di archi di 90° (ovvero quarti di cerchio) questo invece di archi di 108°, il risultato quindi per quanto all'occhio simile, e forse persino indistinguibile, non può essere identico.
- ^ 108° è l'ampiezza dell'angolo del pentagono regolabile ricavabile con la nota formula 180 - (360/n)
- ^ Ottusaureo, su Fiera dell'auro, Tartapelago, 2016.
- ^ Nautilus triaureo, su Fiera dell'aureo, Tartapelago, 2016.
- ^ Chiocciola triaurea, su Fiera dell'aureo, Tartapelago, 2016.
- ^ Emanuela Flammini, Sulle tassellazioni di Penrose (PDF), su mat.uniroma3.it..
- ^ Penrose, su Zibaldone scientifico, zibalsc.blogspot.com..
Altri progetti
Altri progetti
- Wikimedia Commons
 Wikimedia Commons contiene immagini o altri file su triangolo aureo
Wikimedia Commons contiene immagini o altri file su triangolo aureo
Collegamenti esterni
- (EN) Eric W. Weisstein, Triangolo aureo, su MathWorld, Wolfram Research.

- Giorgio Pietrocola Animazione sulla reciprocità dei triangoli aurei
 Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica
Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica









![Rombi di Penrose[9]](http://upload.wikimedia.org/wikipedia/commons/thumb/c/cf/Duerombi.gif/120px-Duerombi.gif)


![Dardi e aquiloni[10]](http://upload.wikimedia.org/wikipedia/commons/thumb/4/4c/DardoAquilone.gif/120px-DardoAquilone.gif)












