Jumlah Riemann

Dalam matematika, jumlah Riemann adalah salah satu jenis aproksimasi/hampiran integral menggunakan metode penjumlahan terbatas. Nama metode ini berasal dari seorang ahli matematika Jerman di abad ke-19 bernama Bernhard Riemann.^[1] Salah satu aplikasi jumlah Riemann yang sangat umum digunakan adalah penghampiran luas daerah suatu fungsi atau garis pada grafik, panjang kurva, dan perkiraan lainnya.

Jumlah Riemann dihitung dengan mempartisi (membagi) daerah yang ingin dihitung menjadi beberapa keping dengan bentuk tertentu (persegi panjang, trapesium, parabola, atau kubik). Luas dari semua kepingan tersebut kemudian dihitung dan dijumlahkan.^[2] Metode ini dapat digunakan untuk menentukan aproksimasi numerik integral tentu, bahkan ketika teorema dasar kalkulus membuatnya tidak mudah untuk menemukan solusi bentuk tertutup .

Karena kepingan-kepingan kecil tersebut tidak selalu tepat menutupi semua daerah yang diukur, luas daerah yang dihitung menggunakan jumlah Riemann akan berbeda dari luas sebenarnya. Kesalahan ini dapat diminimalisasi dengan membagi wilayah menjadi kepingan yang lebih kecil dalam jumlah yang lebih banyak. Saat kepingan semakin kecil, luas yang didapat melalui hampiran ini akan semakin mendekati integral Riemann.^[3]

Definisi

Apabila diberikan ${\displaystyle f:[a,b]\rightarrow \mathbb {R} }$ sebagai fungsi yang didefinisikan pada interval tertutup ${\displaystyle [a,b]}$ bilangan real ${\displaystyle \mathbb {R} }$,

${\displaystyle P=\left\{[x_{0},x_{1}],[x_{1},x_{2}],\dots ,[x_{n-1},x_{n}]\right\}}$,

sebagai partisi dari interval I, dan

${\displaystyle a=x_{0}<x_{1}<x_{2}<\cdots <x_{n}=b}$,

maka jumlah Riemann ${\displaystyle S}$ dari f pada interval I dengan partisi P didefinisikan sebagai

${\displaystyle S=\sum _{i=1}^{n}f({\overline {x_{i}}})\,\Delta x_{i}}$

dengan ${\displaystyle \Delta x_{i}=x_{i}-x_{i-1}}$ dan ${\displaystyle {\overline {x_{i}}}\in [x_{i-1},x_{i}]}$.^[4] Berapapun nilai titik wakil ${\displaystyle {\overline {x_{i}}}}$ tidak begitu penting karena lebar dari ${\displaystyle \Delta x_{i}}$ mendekati nol. Dengan kata lain, anda dapat memilih titik wakil ${\displaystyle {\overline {x_{i}}}}$ berapapun selama nilai yang anda pilih masih berada pada interval ${\displaystyle [x_{i-1},x_{i}]}$ atau ${\displaystyle x_{i-1}\leq {\overline {x_{i}}}\leq x_{i}}$. Jumlah Riemann fungsi f yang didefinisikan pada interval I dan partisi tetap P bernilai sama dan tidak bergantung pada berapa nilai ${\displaystyle {\overline {x_{i}}}}$ yang dipilih.^[5]

Beberapa jenis jumlah Riemann

Terdapat beberapa jenis jumlah Riemann, tergantung pada bagaimana cara memilih titik wakil ${\displaystyle x_{i}^{*}}$:

• Jika ${\displaystyle {\overline {x_{i}}}=x_{i-1}}$ untuk semua i, maka S disebut aturan kiri^[6][7] atau jumlah Riemann kiri.
• Jika ${\displaystyle {\overline {x_{i}}}=x_{i}}$ untuk semua i, maka S disebut aturan kanan^[6][7] atau jumlah Riemann kanan.
• Jika ${\displaystyle {\overline {x_{i}}}=(x_{i}+x_{i-1})/2}$ untuk semua i, maka S disebut aturan titik tengah^[6][7] atau jumlah Riemann tengah.
• Jika ${\displaystyle f({\overline {x_{i}}})=\sup f([x_{i-1},x_{i}])}$ (supremum f pada interval ${\displaystyle [x_{i-1},x_{i}]}$), maka S didefinisikan sebagai jumlah Riemann atas atau jumlah Darboux atas.
• Jika ${\displaystyle f({\overline {x_{i}}})=\inf f([x_{i-1},x_{i}])}$ (infimum f pada interval ${\displaystyle [x_{i-1},x_{i}]}$), maka S didefinisikan sebagai jumlah Riemann bawah atau jumlah Darboux bawah.

Semua metode ini merupakan cara-cara paling sederhana untuk menentukan integrasi numerik. Sebuah fungsi dapat dihitung menggunakan integral Riemann apabila besar jumlah Riemann semakin mendekati suatu nilai tertentu seiring dengan semakin banyaknya partisi.

Metode

Metode-metode penjumlahan Riemann biasanya paling baik dihampiri dengan partisi berukuran sama. Oleh karena itu, interval [${\displaystyle a}$, ${\displaystyle b}$] dibagi menjadi ${\displaystyle n}$ subinterval, masing-masing panjangnya^[8]

${\displaystyle \Delta x={\frac {b-a}{n}}.}$

Titik-titik di partisi akan menjadi

${\displaystyle a,a+\Delta x,a+2\,\Delta x,\ldots ,a+(n-2)\,\Delta x,a+(n-1)\,\Delta x,b.}$

Jumlah Riemann kiri^[9]

Untuk jumlah Riemann kiri, aproksimasi fungsi dihitung menggunakan nilai pada titik ujung kiri dari beberapa persegi panjang dengan alas Δx dan tinggi f(a + iΔx). Menggunakan metode ini dengan i = 0, 1, ..., n - 1 dan menambahkan area yang dihasilkan akan memberi

${\displaystyle A_{\mathrm {kiri} }=\Delta x\left[f(a)+f(a+\Delta x)+\cdots +f(b-\Delta x)\right].}$

Jumlah Riemann kiri akan terlalu besar jika f menurun secara monoton pada interval yang ditentukan dan terlalu kecil jika f meningkat secara monoton.

Jumlah Riemann kanan^[9]

Pada metode Riemann kanan, f dihampiri menggunakan nilai pada titik ujung kanan dari beberapa persegi panjang yang memiliki alas Δx dan tinggi f(a + iΔx). Menggunakan metode ini dengan i = 1, ..., n kemudian menjumlahkan semua luas persegi panjang akan menghasilkan

${\displaystyle A_{\mathrm {kanan} }=\Delta x\left[f(a+\Delta x)+f(a+2\,\Delta x)+\cdots +f(b)\right].}$

Besar jumlah Riemann akan terlalu terlalu kecil jika f menurun secara monoton dan terlalu besar jika f meningkat secara monoton. Galat dari metode ini adalah

${\displaystyle \left\vert \int _{a}^{b}f(x)\,dx-A_{\mathrm {kanan} }\right\vert \leq {\frac {M_{1}(b-a)^{2}}{2n}}}$ ,

dengan ${\displaystyle M_{1}}$ adalah nilai maksimum dari nilai absolut ${\displaystyle f^{\prime }(x)}$ pada interval yang ditentukan.

Aturan Riemann tengah^[9]

Hampiran f pada titik tengah interval memberikan f(a + Δx/2) untuk interval pertama, f(a + 3Δx/2) untuk interval berikutnya, dan seterusnya hingga f(b - Δx/2). Menjumlahkan semua persegi panjang memberi

${\displaystyle A_{\mathrm {tengah} }=\Delta x\left[f(a+{\tfrac {\Delta x}{2}})+f(a+{\tfrac {3\,\Delta x}{2}})+\cdots +f(b-{\tfrac {\Delta x}{2}})\right]}$ .

Galat dari metode ini adalah

${\displaystyle \left\vert \int _{a}^{b}f(x)\,dx-A_{\mathrm {tengah} }\right\vert \leq {\frac {M_{2}(b-a)^{3}}{24n^{2}}}}$ ,

dengan ${\displaystyle M_{2}}$ adalah nilai maksimum dari nilai mutlak ${\displaystyle f^{\prime \prime }(x)}$ pada interval.

Aturan trapesium^[10]

Pada metode ini, nilai-nilai fungsi f pada suatu interval dihampiri dengan nilai rata-rata dari titik akhir kiri dan kanan. Penghitungan menggunakan rumus luas trapesium

${\displaystyle A={\tfrac {1}{2}}h(b_{1}+b_{2})}$

dengan sisi paralel b₁, b₂ dan tinggi h menghasilkan

${\displaystyle A_{\mathrm {trap} }={\tfrac {1}{2}}\,\Delta x\left[f(a)+2f(a+\Delta x)+2f(a+2\,\Delta x)+\cdots +f(b)\right].}$

Galat dari rumus ini adalah

${\displaystyle \left\vert \int _{a}^{b}f(x)\,dx-A_{\mathrm {trap} }\right\vert \leq {\frac {M_{2}(b-a)^{3}}{12n^{2}}},}$

dengan ${\displaystyle M_{2}}$ adalah nilai maksimum dari nilai absolut ${\displaystyle f^{\prime \prime }(x)}$.

Hampiran yang diperoleh menggunakan aturan trapesium untuk suatu fungsi sama dengan rata-rata jumlah Riemann kiri dan kanan dari fungsi tersebut.

Hubungan dengan integrasi

Pada jumlah Riemann satu dimensi dengan domain ${\displaystyle [a,b]}$, ukuran partisi yang semakin kecil hingga mendekati nol akan menyebabkan jumlah Riemann mendekati (konvergen) sebuah nilai tertentu. Nilai limit yang didasarkan pada kondisi ini dapat didefinisikan sebagai integral Riemann dari sebuah fungsi pada domain tertentu,^[11]

${\displaystyle \int _{a}^{b}\!f(x)\,dx=\lim _{\|P\|\rightarrow 0}\sum _{i=1}^{n}f({\overline {x_{i}}})\,\Delta x_{i}}$

${\displaystyle \int _{a}^{b}\!f(x)\,dx=\lim _{n\to \infty }\sum _{i=1}^{n}f({\overline {x_{i}}})\,\Delta x_{i}}$

Pada domain berhingga, ukuran elemen partisi yang menyusut ke nol (${\displaystyle \|P\|\to 0}$) berarti jumlah elemen partisi mencapai tak hingga (${\displaystyle n\to \infty }$). Pada partisi dengan jumlah berhingga, jumlah Riemann akan selalu menjadi hampiran terhadap nilai limit. Hampiran ini akan menjadi lebih akurat apabila partisi semakin kecil dan banyak. Animasi berikut mampu menggambarkan bagaimana partisi yang semakin banyak dapat semakin baik menghampiri luas suatu daerah di bawah kurva

• 
  Riemann kiri
• 
  Riemann kanan
• 
  Riemann tengah

Contoh

• 
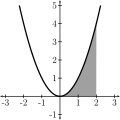  Visualisasi daerah di bawah kurva y = x² pada interval 0 hingga 2. Menggunakan antiturunan, luas daerah ini ditemukan tepat sebesar 8/3.
• 
  Menghampiri daerah di bawah ${\displaystyle y=x^{2}}$ dari 0 hingga 2 menggunakan Riemann kanan.
• 
  Jumlah Riemann di bawah kurva y = x² dari 0 hingga 2. Ketika jumlah persegi panjang semakin banyak, luas area yang diperoleh semakin mendekati angka 8/3.

Ambil contoh persoalan di atas. Luas daerah di bawah kurva y = x² antara 0 dan 2 dapat dihitung menggunakan metode Riemann (dalam contoh ini akan digunakan metode Riemann kanan).

Pertama-tama, interval [0, 2] dibagi menjadi n subinterval yang masing-masing memiliki lebar ${\displaystyle {\tfrac {2}{n}}}$. Lebar subinterval tersebut merupakan lebar dari persegi panjang Riemann (selanjutnya disebut "kepingan"). Karena contoh ini menggunakan Riemann kanan, maka urutan koordinat x untuk kepingan-kepingan tersebut adalah ${\displaystyle x_{1},x_{2},\ldots ,x_{n}}$. Oleh karena itu, ketinggian kepingan secara berturut-turut adalah ${\displaystyle x_{1}^{2},x_{2}^{2},\ldots ,x_{n}^{2}}$. Pada kasus ini, ${\displaystyle x_{i}={\tfrac {2i}{n}}}$ dan ${\displaystyle x_{n}=2}$ .

Luas masing-masing kepingan adalah ${\displaystyle {\tfrac {2}{n}}\times x_{i}^{2}}$. Oleh karena, jumlah Riemann kanan ke-n adalah:

${\displaystyle {\begin{aligned}S&={\frac {2}{n}}\times \left({\frac {2}{n}}\right)^{2}+\cdots +{\frac {2}{n}}\times \left({\frac {2i}{n}}\right)^{2}+\cdots +{\frac {2}{n}}\times \left({\frac {2n}{n}}\right)^{2}\\&={\frac {8}{n^{3}}}\left(1+\cdots +i^{2}+\cdots +n^{2}\right)\\&={\frac {8}{n^{3}}}\left({\frac {n(n+1)(2n+1)}{6}}\right)\\&={\frac {8}{n^{3}}}\left({\frac {2n^{3}+3n^{2}+n}{6}}\right)\\&={\frac {8}{3}}+{\frac {4}{n}}+{\frac {4}{3n^{2}}}\end{aligned}}}$

Apabila digunakan limit n menuju tak hingga, maka dapat ditemukan nilai hampiran yang mendekati nilai luas daerah di bawah kurva yang sebenarnya:

${\displaystyle \lim _{n\to \infty }S=\lim _{n\to \infty }\left({\frac {8}{3}}+{\frac {4}{n}}+{\frac {4}{3n^{2}}}\right)={\frac {8}{3}}}$

Hasil yang diperoleh menggunakan metode ini sama dengan hasil yang diperoleh menggunakan metode integral tentu:

${\displaystyle \int _{0}^{2}x^{2}\,dx={\frac {8}{3}}}$

Dimensi yang lebih tinggi

Gagasan dasar di balik metode penjumlahan Riemann adalah "memecah-mecah" domain menjadi beberapa bagian, menghitung "ukuran" dari setiap bagian, kemudian menjumlahkan semua ukuran yang didapat. Melalui gagasan ini, metode jumlah Riemann dapat digeneralisasi untuk menghitung fungsi dengan domain lebih dari satu dimensi. Meskipun demikian, detail teknis tentang bagaimana domain dapat dipartisi menjadi jauh lebih rumit daripada kasus satu dimensi dan melibatkan aspek bentuk geometris domain.^[12]

Dua dimensi

Pada kasus dua dimensi, domain ${\displaystyle A}$ dapat dibagi menjadi beberapa bagian ${\displaystyle A_{i}}$ (${\displaystyle A=\cup _{i}A_{i}}$). Setiap bagian kemudian dapat diartikan sebagai memiliki "luas" yang disebut ${\displaystyle \Delta A_{i}}$.^[13] Jumlah Riemann-nya adalah

${\displaystyle S=\sum _{i=1}^{n}f({\overline {x_{i}}},{\overline {y_{i}}})\,\Delta A_{i},}$

dengan ${\displaystyle ({\overline {x_{i}}},{\overline {y_{i}}})\in A_{i}}$ .

Tiga dimensi

Pada kasus tiga dimensi, domain ${\displaystyle V}$ dengan ${\displaystyle V=\cup _{i}V_{i}}$ dan ${\displaystyle \Delta V_{i}}$ adalah "volume" bagian yang diindeks ${\displaystyle i}$. Jumlah Riemann tiga dimensi kemudian dapat dinotasikan sebagai^[14]

${\displaystyle S=\sum _{i=1}^{n}f({\overline {x_{i}}},{\overline {y_{i}}},{\overline {z_{i}}})\,\Delta V_{i}}$

dengan ${\displaystyle ({\overline {x_{i}}},{\overline {y_{i}}},{\overline {z_{i}}})\in V_{i}}$ .

Dimensi yang lebih tinggi

Jumlah Riemann pada dimensi yang lebih tinggi mengikuti metode serupa pada satu, dua, hingga tiga dimensi. Untuk dimensi n, jumlah Riemann dapat ditulis sebagai^[8]

${\displaystyle S=\sum _{}f({\overline {P_{i}}})\,\Delta V_{i}}$

dengan ${\displaystyle {\overline {P_{i}}}\in {V_{i}}}$, yaitu sebuah titik di bagian n-dimensi ${\displaystyle V_{i}}$ dengan volume n-dimensi ${\displaystyle \Delta V_{i}}$.

Lihat pula

• Antiderivatif
• Integral Lebesgue
• Integral Riemann, limit jumlah Riemann saat partisi yang digunakan berjumlah tak hingga
• Aturan Simpson, metode numerik yang lebih akurat daripada jumlah Riemann dasar atau bahkan aturan Trapesium
• Aturan trapesium, metode numerik berdasarkan rata-rata penjumlahan Riemann kiri dan kanan

Referensi

Pranala luar

• (Inggris) Weisstein, Eric W. "Riemann Sum". MathWorld. 
• Sebuah simulasi yang menampilkan kekonvergenan jumlah Riemann