Rolle-tétel

Nem tévesztendő össze a következővel: Rolle-féle gyöktétel.

A matematikai analízisben a Rolle-tétel vagy Rolle-féle középértéktétel az egyik fontos és gyakran alkalmazott tétel, ami egy intervallumon értelmezett differenciálható függvény „vízszintes” érintőjének (azaz a derivált zérushelyének) létezésére ad elégséges feltételt.

A tétel

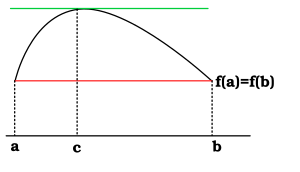
Ha az ${\displaystyle f}$ függvény folytonos az ${\displaystyle [a,b]}$ intervallumban, differenciálható az intervallum belső pontjaiban és

${\displaystyle f(a)=f(b)}$,

akkor van olyan ${\displaystyle a<c<b}$ szám, hogy

${\displaystyle f'(c)=0}$

teljesül.

Bizonyítása

Ha az ${\displaystyle f}$ függvény az ${\displaystyle (a,b)}$ intervallumon végig az ${\displaystyle f(a)=f(b)}$ értéket veszi fel, akkor konstans, tehát deriváltja mindenütt 0.

Tegyük fel, hogy egy pontban ${\displaystyle f}$ értéke ettől eltér. Az általánosság megszorítása nélkül feltehető, hogy ez az érték nagyobb ${\displaystyle f(a)=f(b)}$-nél (ellenkező esetben ugyanezt a gondolatmenetet a ${\displaystyle -f}$ függvényre kell alkalmaznunk). A Weierstrass-tétel szerint a függvény az ${\displaystyle [a,b]}$ intervallumban valahol felveszi maximumát. Legyen ${\displaystyle c}$ egy ilyen pont. ${\displaystyle c}$ nem lehet ${\displaystyle a}$-val vagy ${\displaystyle b}$-vel egyenlő, mert akkor lenne nála nagyobb értékű hely, ami ellentmond ${\displaystyle f(c)}$ maximális tulajdonságának. Mivel ${\displaystyle f}$ a ${\displaystyle c}$-ben (mely az értelmezési tartomány belső pontjában van) differenciálható és ott maximuma van, ezért a szélsőértékekre vonatkozó Fermat-tétel miatt ott a deriváltja 0.

Általánosításai

A Rolle-tétel érvényes tetszőleges intervallumon értelmezett differenciálható függvény esetén is, amennyiben a két végpont függvényértékének egyenlőségét a határértékek egyenlősége váltja fel.

Tétel – Az f : ${\displaystyle I}$${\displaystyle \rightarrow }$R intervallumon értelmezett, belül differenciálható függvény esetén létezik olyan ξ ∈ ${\displaystyle I}$ pont, hogy f '( ξ ) = 0, feltéve, hogy létezik az lim_α f és lim_β f határérték és lim_α f = lim_β f , ahol α és β a ${\displaystyle I}$ két végpontja.

Bizonyítás. Indirekt módon tegyük fel, hogy minden x ∈ int(${\displaystyle I}$) belső pont esetén f '(x) > 0 vagy f '(x) < 0. Ekkor speciálisan az is igaz, hogy minden x ∈ int(${\displaystyle I}$)-re f '(x) > 0 vagy minden x ∈ int( ${\displaystyle I}$ )-re f '(x) < 0, ugyanis ha lenne a < b int(${\displaystyle I}$)-beli elem, hogy f '(a) és f '(b) ellenkező előjelű (nem nulla), akkor a Darboux-tételt alkalmazva lenne olyan c pont az [a,b] zárt halmazon, hogy f '(c) = 0, ami ellentmond az indirekt feltételnek. Ha ezzel szemben f az int(${\displaystyle I}$) halmazon állandó előjelű, akkor szigorúan monoton, ami meg annak mond ellent, hogy lim_α f = lim_β f, tehát mindenképpen ellentmondásra jutunk.

Ilyen például az

${\displaystyle x\mapsto e^{-x^{2}}}$

függvény.

Egy másik általánosítás a differenciálhatósági feltételen lazít.

Tétel – Ha az f : [a,b]${\displaystyle \rightarrow }$R korlátos, zárt intervallumon értelmezett folytonos függvény olyan, hogy f(a) = f(b) és az I minden belső pontjában vagy differenciálható f, vagy a különbségi hányadosnak létezik +∞ vagy -∞ értékű határértéke, akkor létezik olyan ξ ∈ int(${\displaystyle I}$) pont, hogy f '(ξ) = 0.

Ilyen például a [-2,2]-n értelmezett

${\displaystyle x\mapsto \mathrm {sgn} (1-x^{2}){\sqrt {|1-x^{2}|}}}$

függvény.

A tétel fontos általánosítása még a Lagrange-féle középértéktétel is, mely (a tétel jelöléseivel)

${\displaystyle {\frac {f(b)-f(a)}{b-a}}}$

meredekségű érintő létezésére ad elégséges feltételt (f(b)=f(a) esetén persze megkapjuk a Rolle-tételt).

Források

• Komornik Vilmos: Valós analízis előadások I-II. Typotex Kiadó, 2003. ISBN 963-9548-21-9, ISBN 963-9548-22-7

További információk

• A PlanetMath Rolle's theorem szócikke

A Wikimédia Commons tartalmaz Rolle-tétel témájú médiaállományokat.