Moment quadratique

Le moment quadratique est une grandeur qui caractérise la géométrie d'une section et se définit par rapport à un axe ou un point. Il s'exprime dans le Système international en m⁴ (mètre à la puissance 4, ou mètre bicarré ^[1]).

Le moment quadratique est utilisé en résistance des matériaux, il est indispensable pour calculer la résistance et la déformation des poutres sollicitées en torsion (${\displaystyle I_{G}}$) et en flexion (${\displaystyle I_{x}}$ et ${\displaystyle I_{y}}$). En effet, la résistance d'une section sollicitée selon un axe donné varie avec son moment quadratique selon cet axe.

Le moment quadratique est encore trop souvent appelé moment d'inertie. A tort^[1], car s'il présente de claires similitudes avec le moment d'inertie, il ne rend compte que de la répartition de la matière en son sein.

Définition générale

« Le moment quadratique axial d'une aire plane (section) par rapport à un axe situé dans son plan est la somme (intégrale) des produits de ses éléments par les carrés de leurs distances à l'axe. Le moment quadratique polaire d'une aire plane (section) par rapport à un point situé dans son plan est la somme (intégrale) des produits de ses éléments par les carrés de leurs distances au point. »^[1]

• Moment quadratique de la section ${\displaystyle S}$ par rapport à l’axe ${\displaystyle \mathrm {O} {\vec {x}}}$ :

${\displaystyle I_{x}=\iint _{S}y^{2}\,\mathrm {d} s=\iint _{S}y^{2}\,\mathrm {d} x\,\mathrm {d} y}$

• Moment quadratique de la section ${\displaystyle S}$ par rapport à l’axe ${\displaystyle \mathrm {O} {\vec {y}}}$ :

${\displaystyle I_{y}=\iint _{S}x^{2}\,\mathrm {d} s=\iint _{S}x^{2}\,\mathrm {d} x\,\mathrm {d} y}$

• Moment quadratique (polaire) de ${\displaystyle S}$ par rapport au point-origine ${\displaystyle \mathrm {O} }$ :

${\displaystyle I_{\mathrm {O} }=\iint _{S}r^{2}\,\mathrm {d} s=\iint _{S}r^{2}\,\mathrm {d} x\,\mathrm {d} y=I_{x}+I_{y}}$

puisque ${\displaystyle r^{2}=x^{2}+y^{2}}$ (théorème de Pythagore). I_O peut aussi être qualifié de moment quadratique par rapport à l'axe ${\displaystyle \mathrm {O} {\vec {z}}}$ (perpendiculaire au plan de la section), et noté I_z.

Il découle de ces définitions que plus les éléments de la section sont situés loin de l'axe, plus le moment quadratique est important.

Application de la définition

Pour une section carrée de côté ${\displaystyle a}$ centrée en ${\displaystyle \mathrm {O} }$ :

• Moment quadratique par rapport à ${\displaystyle \mathrm {O} {\vec {x}}}$ :

${\displaystyle {\begin{aligned}I_{x}&=\iint _{S}y^{2}\,\mathrm {d} x\,\mathrm {d} y=\left(\int _{-{\frac {a}{2}}}^{\frac {a}{2}}\mathrm {d} x\right)\cdot \left(\int _{-{\frac {a}{2}}}^{\frac {a}{2}}y^{2}\,\mathrm {d} y\right)\\&=\left[{\frac {a}{2}}-\left(-{\frac {a}{2}}\right)\right]\cdot {\frac {1}{3}}\left[\left({\frac {a}{2}}\right)^{3}-\left(-{\frac {a}{2}}\right)^{3}\right]={\frac {1}{3}}a\left({\frac {a^{3}}{8}}+{\frac {a^{3}}{8}}\right)\\&={\frac {a^{4}}{12}}\end{aligned}}}$

• Moment quadratique par rapport à ${\displaystyle \mathrm {O} {\vec {y}}}$ :

Par un calcul similaire, ou plus simplement en raison de la symétrie de la section :

${\displaystyle I_{y}=I_{x}={\frac {a^{4}}{12}}}$

• Moment quadratique par rapport au point ${\displaystyle \mathrm {O} }$ :

Comme ${\displaystyle I_{\mathrm {O} }=I_{x}+I_{y}}$ :

${\displaystyle I_{\mathrm {O} }={\frac {a^{4}}{6}}}$

Formules pour les sections usuelles

Section rectangulaire

${\displaystyle I_{x}={\frac {b\,h^{3}}{12}}}$

${\displaystyle I_{y}={\frac {h\,b^{3}}{12}}}$

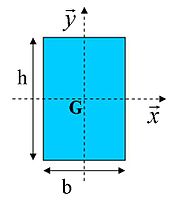
${\displaystyle I_{\mathrm {G} }=\alpha b^{3}h}$ où α dépend de l'élancement de la section^[2] (cf. Torsion).

Section circulaire

${\displaystyle I_{x}=I_{y}={\frac {\pi D^{4}}{64}}}$

${\displaystyle I_{\mathrm {G} }={\frac {\pi D^{4}}{32}}}$

Section annulaire

Il s'agit simplement de soustraire le moment quadratique du disque intérieur à celui du disque extérieur.

${\displaystyle I_{x}=I_{y}={\frac {\pi }{64}}(D^{4}-d^{4})}$

${\displaystyle I_{\mathrm {G} }={\frac {\pi }{32}}(D^{4}-d^{4})}$

Formule de transport

Le moment quadratique d'une section ${\displaystyle S}$ dont le barycentre passe par un axe ${\displaystyle \Delta }$ parallèle à un axe de référence ${\displaystyle \Delta '}$ à une distance ${\displaystyle d}$ vaut, d'après le théorème de transport de Huygens :

${\displaystyle I_{\Delta '}=I_{\Delta }+S\cdot d^{2}}$.

Ceci exprime que le moment quadratique est égal à la somme du « moment propre » ${\displaystyle I_{\Delta }}$ et du « moment de translation » ${\displaystyle S.d^{2}}$.

Exemple pour une section complexe

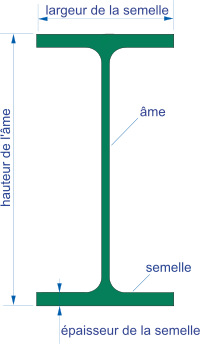
Poutre en I

On décompose la poutre en 3 parties, les deux semelles et l'âme. On fait la somme des moments quadratiques de chaque section. Si on choisit l'axe neutre comme axe de rotation, on doit utiliser le théorème des axes parallèles (transport) pour le moment quadratique des semelles :

${\displaystyle I_{\text{x}}=I_{1}+2I_{2}={\frac {e(h-2e')^{3}}{12}}+2({\frac {l'e'^{3}}{12}}+(l'e').({\frac {h}{2}}-{\frac {e'}{2}})^{2})}$

avec ${\displaystyle e}$ et ${\displaystyle h}$ l'épaisseur et la hauteur de l’âme et ${\displaystyle l'}$ et ${\displaystyle e'}$ la largeur et l'épaisseur d'une semelle.

Il est également possible de considérer une section rectangulaire de largeur ${\displaystyle l'}$ et de hauteur ${\displaystyle h}$ à laquelle il faut soustraire l'inertie de la portion considérée en trop, soit une autre section rectangulaire de largeur ${\displaystyle l'-e}$ et de hauteur ${\displaystyle h-2e'}$. La formule devient alors :

${\displaystyle I_{\text{x}}=I_{1}-I_{2}={\frac {b_{1}h_{1}^{3}}{12}}-{\frac {b_{2}h_{2}^{3}}{12}}={\frac {l'h^{3}}{12}}-{\frac {(l'-e)(h-2e')^{3}}{12}}}$

Les semelles sont les parties qui subissent la plus grande déformation. Ces parties sont donc plus larges, afin d'offrir une meilleure résistance à la déformation, tout en réduisant l'âme afin de gagner du poids. L'âme sert à écarter les semelles afin d'augmenter leur moment quadratique. Ainsi, à aire équivalente, le moment quadratique d'une section en I est beaucoup plus grand que celui d'une section carrée, d'autant plus que les épaisseurs — surtout celle de l'âme — sont faibles.

Ces poutres sont donc largement utilisées en génie civil et en mécanique car elles permettent des économies de matière.

Application aux composites, sandwich

En utilisant pour ces parties un matériau plus résistant aux contraintes (cf. Déformation élastique) ou ayant un module de Young plus élevé, on peut donc considérablement augmenter ses caractéristiques mécaniques. Pour l'âme, on peut alors utiliser un matériau de résistance moindre mais plus léger, celui-ci étant soumis à de moins grandes déformations.

Ce principe est utilisé abondamment dans la fabrication de bateaux en matériaux composites : l'âme est faite en mousse ou dans un matériau de faible densité (par exemple un polymère ou du balsa) et les semelles sont en fibres (verre, carbone, …). Ce type de fabrication est appelé sandwich dans le milieu nautique, à cause de cette structure en 3 feuilles superposées.

Références

Voir aussi

Articles connexes

• Théorie des poutres, Flexion pure

• Portail de la physique