Topología cociente

En matemáticas, la topología cociente consiste intuitivamente en crear una topología pegando ciertos puntos sobre otros, en un espacio dado, por medio de una relación de equivalencia bien definida. El nuevo espacio así generado recibe el nombre de espacio cociente. Ejemplos conocidos son el toro matemático o la banda de Möbius.
Definición
Sean un espacio topológico y una relación de equivalencia sobre . El conjunto cociente es el conjunto de clases de equivalencia de los elementos de :
Los conjuntos abiertos que conforman la llamada topología cociente sobre son los conjuntos de las clases de equivalencia cuyas uniones son conjuntos abiertos en :
Definición equivalente: sea la aplicación proyección dada por , se definen los abiertos de como los conjuntos tales que es abierto. Es decir, un conjunto de clases de equivalencia es abierto si los elementos que las forman son un conjunto abierto de la topología original.
| es, en efecto, una topología. (Según la definición equivalente) |
| ya que , que es un abierto de por definición de topología. ya que , que es un abierto de por definición de topología. Dados abiertos de , tenemos que por definición de topología cociente. Por ser topología, , pero . Dados abiertos de , tenemos que por definición de topología cociente. Por ser topología, , pero . |
Propiedades
- La aplicación proyección al cociente que envía a cada elemento a su clase de equivalencia correspondiente es continua[1]y la topología cociente es la más fina que se puede definir en que cumple esto. Es decir, la topología cociente es la topología final respecto a la proyección al cociente.
| Demostración |
| Claramente, la topología cociente hace la proyección al cociente continua. En efecto, para ver que es continua, tomamos abierto y vemos que su antiimagen por es abierta de . Pero por ser abierto de la topología cociente, por definición, es un abierto, que es lo que queríamos. Que es la más fina que lo cumple también es inmediato por definición. Si es una topología de más fina que , por definición, necesariamente tiene un abierto con no abierto de , y esto contradice la definición de continuidad. |
- Sean la proyección al cociente y una aplicación. Entonces, la aplicación es continua si, y sólo si, la composición es continua.[1]
| Demostración |
| Como es continua por hipótesis y ya se ha demostrado que es continua, es continua por ser composición de aplicaciones continuas. Sea abierto y veamos que su antiimagen por , , es un abierto de . Esto es equivalente, por definición de topología cociente, a ver que es un abierto de , pero esto es cierto por ser continua, por hipótesis. |
- La propiedad universal: La topología cociente es la única topología que cumple que para cualquier espacio topológico (Z, T) y cualquier función g:(Y, ) (Z, T) se tiene que g es continua si y sólo si es continua
Ejemplos
En los siguientes ejemplos los homeomorfismos se construyen primero deformando el espacio cociente sin tener en cuenta la relación de equivalencia (cortándola) y después pegando los trozos que estaban relacionados. Es decir, estamos admitiendo que podemos construir un espacio entre dos espacios cociente a partir de uno entre los espacios originales siempre y cuando los elementos relacionados antes y después del homeomorfismo sean los mismos. Este resultado, que justifica que las construcciones siguientes son correctas, se conoce como lema de cortar y pegar, y se demuestra a continuación
| Lema de cortar y pegar: Sea un homeomorfismo y relaciones de equivalencia en e , respectivamente, que satisfacen que . Entonces, la aplicación dada por está bien definida y es un homeomorfismo. |
| Está bien definida: sean y veamos que la imagen por de su clase de equivalencia no depende de cuál tomemos como representante. En efecto, , que es lo que queríamos. es exhaustiva: Sea , con representante . Como es homeomorfismo y, en particular, exhaustiva, tal que . Pero entonces y tenemos una antiimagen de . es inyectiva: Supongamos que y veamos que . En efecto, . es continua. Sean las proyecciones a , respectivamente. Tenemos que : En efecto, dado , . Pero es continua por ser homeomorfismo y por ser una proyección al cociente. Por tanto, también lo es la composición , pero por la segunda propiedad del apartado de propiedades esto quiere decir que es continua. es continua. La demostración es la misma que pero heredando continuidad de (continua por ser homeomorfismo). |
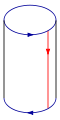
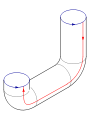
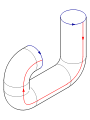
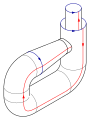
- El toro como conjunto cociente:[1] Sobre se define la relación de equivalencia y . El espacio cociente es homeomorfo a un toro.
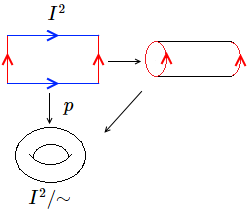
Toro
- La banda de Möbius como conjunto cociente:[1] Sobre se define la relación de equivalencia . El espacio cociente es homeomorfo a una banda de Möbius.

Banda de Möbius
- La botella de Klein como conjunto cociente:[2] Sobre se define la relación de equivalencia y . El espacio cociente es homeomorfo a una botella de Klein (es difícil de visualizar puesto que no es homeomorfo a un subespacio de ).
- La esfera como conjunto cociente:[3] Sobre (cuadrado de vértices ) se define la relación de equivalencia para de la frontera. El espacio cociente correspondiente es homeomorfo a una esfera.
Referencias
Bibliografía
- Robles Corbalá Carlos Alberto, "Topología general" primera edición Universidad de Sonora.
- Weisstein, Eric W. «Espacio cociente». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Quotient space en PlanetMath.
- Hazewinkel, Michiel, ed. (2001), «Quotient_space&oldid=11882», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .
Enlaces externos
- López Camino, Rafael. «Capítulo 7. espacios cocientes» (PDF). Universidad de Granada. Archivado desde el original el 14 de agosto de 2011. Consultado el 30 de abril de 2011.
 Wikilibros alberga un libro o manual sobre Espacios Métricos/Productos y Cocientes. incluyendo un capítulo sobre espacios cocientes.
Wikilibros alberga un libro o manual sobre Espacios Métricos/Productos y Cocientes. incluyendo un capítulo sobre espacios cocientes.
 Datos: Q77981916
Datos: Q77981916




![{\displaystyle Y=\{[x]:x\in X\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be56fce8ca3c36a3fe823a5bf46561e96aaeb74d)


![{\displaystyle {\mathcal {T}}_{\sim }=\{U\subseteq Y:\bigcup _{[x]\in U}[x]\in {\mathcal {T}}_{X}\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24f673d58c8110d2b99bde81aced90947e7f25ec)

![{\displaystyle p(x)=[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24b8773dff8ad19fc5a8f33134a4da367b04fc0c)











































![{\displaystyle [x]_{X}\mapsto f_{\sim }([x]_{X})=[f(x)]_{Y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae7babc576c0e9d5a5cc5ca7560b5240e32cfdc)


![{\displaystyle [x]_{X}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffaba5909fe85603ae2ac02a82d9a40023775ff4)
![{\displaystyle x\sim _{X}x'{\overset {\text{Hipótesis}}{\Rightarrow }}f(x)\sim _{Y}f(x')\Rightarrow [f(x)]_{Y}=[f(x')]_{Y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d73455deee1e90d6ddb2db714f008129202c0ce)
![{\displaystyle [y]_{Y}\in Y/{\sim _{Y}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e2e45e02deb31b84260019389f40a88eef35752)



![{\displaystyle [y]_{Y}=[f(x)]_{Y}=f_{\sim }([x]_{X})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2a30145abf81e4020e7b57c6c2e74953bd48e1f)
![{\displaystyle [y]_{Y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0abce24890864d483c4b91a6197bf6ad8d13897)
![{\displaystyle f_{\sim }([x]_{X})=f_{\sim }([x']_{X})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72d22502468615e25c1efc7ef402ef6c72a8e9f2)
![{\displaystyle [x]_{X}=[x']_{X}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/feb13314d07e316bd2bf3f180935182c268461ae)
![{\displaystyle f_{\sim }([x]_{X})=f_{\sim }([x']_{X})\Rightarrow [f(x)]_{Y}=[f(x')]_{Y}\Rightarrow f(x)\sim _{Y}f(x'){\overset {\text{Hipótesis}}{\Rightarrow }}x\sim _{X}x'\Rightarrow [x]_{X}=[x']_{X}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4006ac71740b67716f0cb2354e50921e5ad14804)




![{\displaystyle \pi _{Y}(f(x))=[f(x)]_{Y}{\overset {\text{def}}{=}}f_{\sim }([x]_{X})=f_{\sim }(\pi _{X}(x))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfe3a31dc985d5d27a2a24b58fcf7d5727df129e)



![{\displaystyle I^{2}=[0,1]\times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec146272a9e354527468cb89f8213c57e07c937e)

![{\displaystyle (0,y)\sim (1,y)\quad \forall x,y\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6927082a10804df2a21ae760b47db2326ffde5cb)



![{\displaystyle (0,y)\sim (1,1-y)\quad \forall y\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1025c37e0ba2db5a59f2a2a835744b1ff7d7178)

![{\displaystyle (0,y)\sim (1,1-y)\quad \forall x,y\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14976476db9bc4252b7394480d9d425f956bca2f)