Regula falsi

Regula-falsi-Verfahren (lateinisch regula falsi ‚Regel des Falschen‘), auch: Regula duarum falsarum Positionum (lateinisch regula duarum falsarum positionum ‚Regel vom zweifachen falschen Ansatz‘),^[1][2] Falsirechnung rsp. Falsi-Rechnung sind Methoden zur Berechnung von Nullstellen.

• Die ursprüngliche, historische Regula Falsi diente der Lösung einer linearen Gleichung mit Hilfe zweier „falscher“ Testwerte.
• Als numerische Methode, auch lineares Eingabeln genannt, dient die Regula Falsi als Iterationsmethode zur Ermittlung der Nullstelle reeller Funktionen. Sie kombiniert Methoden vom Sekantenverfahren und der Bisektion.

Das Regula-falsi-Verfahren startet mit zwei Stellen (in der Nähe der Nullstelle) ${\displaystyle a_{0}}$ und ${\displaystyle b_{0}}$, deren Funktionsauswertungen ${\displaystyle f(a_{0})}$, ${\displaystyle f(b_{0})}$ unterschiedliche Vorzeichen haben. In dem Intervall ${\displaystyle [a,b]}$ befindet sich somit nach dem Zwischenwertsatz (für stetiges ${\displaystyle f}$) eine Nullstelle. Nun verkleinert man in mehreren Iterationsschritten das Intervall und bekommt so eine immer genauere Näherung für die Nullstelle.

In Schritt ${\displaystyle k}$ berechnet man:

${\displaystyle \!\,c_{k}=a_{k-1}-{\frac {b_{k-1}-a_{k-1}}{f(b_{k-1})-f(a_{k-1})}}f(a_{k-1})}$  ${\displaystyle \!\,={\frac {a_{k-1}{f(b_{k-1})}-b_{k-1}{f(a_{k-1})}}{f(b_{k-1})-f(a_{k-1})}}}$.

Ist ${\displaystyle f(c_{k})=0}$, so wird das Verfahren beendet, denn mit ${\displaystyle c_{k}}$ ist eine Nullstelle gefunden. Anderenfalls wählt man ${\displaystyle a_{k}}$, ${\displaystyle b_{k}}$ wie folgt:

• ${\displaystyle a_{k}=c_{k},\ b_{k}=b_{k-1}}$ falls ${\displaystyle f(a_{k-1})}$ und ${\displaystyle f(c_{k})}$ gleiches Vorzeichen haben sowie
• ${\displaystyle a_{k}=a_{k-1},\ b_{k}=c_{k}}$ falls ${\displaystyle f(b_{k-1})}$ und ${\displaystyle f(c_{k})}$ gleiches Vorzeichen haben,

und geht damit in den nächsten Iterationsschritt.

• Die Berechnung des ${\displaystyle c_{k}}$ entspricht dem Anwenden des Sekantenverfahrens mit einer Iteration im ${\displaystyle (k-1)}$-ten Intervall. Im Gegensatz zum Sekantenverfahren befindet sich in diesem Intervall aber stets eine Nullstelle.
• Geometrisch kann man ${\displaystyle c_{k}}$ als die Nullstelle der Sekante durch ${\displaystyle \left(a_{k-1},f(a_{k-1})\right)}$ und ${\displaystyle \left(b_{k-1},f(b_{k-1})\right)}$ deuten.
• ${\displaystyle c_{k}}$ liegt natürlich immer im Intervall ${\displaystyle \left[a_{k-1},b_{k-1}\right]}$.
• Konvergenz: Solange ${\displaystyle f}$ im ${\displaystyle k}$-ten Intervall nicht strikt konkav bzw. konvex ist, also im Intervall ein Vorzeichenwechsel der zweiten Ableitung vorliegt, liegt superlineare Konvergenz vor.

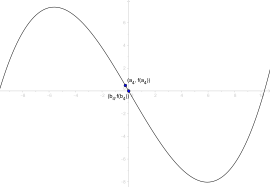
• Visualisierung der Regula falsi
• 
• 
• 
• 
• 

Ist ${\displaystyle f}$ konkav oder konvex im Intervall ${\displaystyle [a_{k},b_{k}]}$, hat die zweite Ableitung also überall im Intervall das gleiche Vorzeichen, so bleibt eine der Intervallgrenzen für alle weiteren Iterationen stehen, denn die Sekante liegt immer unterhalb bzw. oberhalb der Funktion. Die andere Intervallgrenze konvergiert jetzt nur noch linear gegen die Lösung.

Abhilfe schaffen die folgenden Verfahren.

Den verbesserten Verfahren liegt die folgende Idee zu Grunde: Falls sich die „linke“ Intervallgrenze ${\displaystyle x_{1}}$ im aktuellen Schritt nicht verändert – das heißt, dass die tatsächliche Nullstelle zwischen der „linken“ Grenze und der genäherten Nullstelle liegt –, multipliziert man ${\displaystyle f(x_{1})}$ mit einem Faktor ${\displaystyle 0<m<1}$ und bringt den Funktionswert an der Stelle ${\displaystyle x_{1}}$ damit näher an Null.

Entweder verkürzt sich somit der Abstand der Näherung zur Nullstelle im nächsten Schritt oder die Nullstelle wird im nächsten Schritt zwischen der tatsächlichen Nullstelle und der „rechten“ Intervallgrenze genähert.

Im zweiten Fall werden dann einfach „rechts“ und „links“ für den nächsten Schritt vertauscht. Da der zweite Fall irgendwann – auch in konvexen Intervallen – immer eintritt, ist sicher, dass keine der beiden Intervallgrenzen bis zum Abbruch stehen bleibt. Somit ist die Konvergenz garantiert superlinear.

Den folgenden Algorithmus haben diese Verfahren gemeinsam:

${\displaystyle \!\,{\begin{array}{l}{\mathsf {solange}}~\circledast (|x_{2}-x_{1}|\geq \varepsilon _{x},|f_{z}|\geq \varepsilon _{f}):\\~~\left[{\begin{array}{l}z:=x_{1}-{\frac {f_{1}}{s}}~\mathrm {mit} ~s={\frac {f_{2}-f_{1}}{x_{2}-x_{1}}}\\f_{z}:=f(z)\\{\mathsf {falls}}~f_{z}\cdot f_{2}<0:\\~~\left[x_{1}:=x_{2},~f_{1}:=f_{2},~x_{2}:=z,~f_{2}:=f_{z}\right.\\{\mathsf {falls}}~f_{z}\cdot f_{2}>0:\\~~\left[f_{1}:=m\cdot f_{1},~x_{2}:=z,~f_{2}:=f_{z},~x_{1}~{\text{bleibt}}\right.\\{\mathsf {sonst}}:\\~~\left[x_{1}:=z,~f_{1}:=f_{z},~x_{2}:=z,~f_{2}:=f_{z}\right.\\\end{array}}\right.\\~\\{\text{nimm }}z{\text{ als Näherung für }}x^{*}\end{array}}}$

Dabei sind ${\displaystyle x_{1},x_{2}}$ die Intervallgrenzen im ${\displaystyle k}$-ten Schritt, ${\displaystyle f_{1},f_{2}}$ und ${\displaystyle f_{z}}$ die Funktionswerte an den Stellen ${\displaystyle x_{1},x_{2}}$ und ${\displaystyle z}$. ${\displaystyle \varepsilon _{x},\varepsilon _{f}}$ sind die Abbruchgrenzen und ${\displaystyle m}$ der Verkürzungsfaktor. ${\displaystyle \circledast (\cdot ,\cdot )}$ steht hier für eine nicht näher spezifizierte, zweistellige Boolesche Funktion. Sinnvolle Funktionen wären hier die Disjunktion, die Konjunktion, die Identität des ersten und die Identität des zweiten Operanden. Im ersten Fall muss eine der beiden Abbruchgrenzen, im zweiten Fall beide, im dritten Fall lediglich ${\displaystyle \varepsilon _{x}}$ und im vierten Fall ${\displaystyle \varepsilon _{f}}$ unterschritten werden, damit ${\displaystyle \circledast (|x_{2}-x_{1}|\geq \varepsilon _{x},|f_{z}|\geq \varepsilon _{f})}$ falsch wird und das Verfahren abbricht.

Die unterschiedlichen Verfahren unterscheiden sich lediglich im Verkürzungsfaktor ${\displaystyle m}$.

Illinois-Verfahren

${\displaystyle m_{I}=0{,}5}$

Pegasus-Verfahren

${\displaystyle m_{P}={\frac {f_{2}}{f_{2}+f_{z}}}}$

Anderson/Björck-Verfahren

${\displaystyle m_{A/B}={\begin{cases}1-{\frac {f_{z}}{f_{2}}}&{\text{falls}}~1-{\frac {f_{z}}{f_{2}}}>0\\0{,}5&{\text{sonst}}\end{cases}}}$

Die zu untersuchende Funktion und die Abbruchkriterien:

epsx, epsf seien definiert
f(x) sei definiert

Der Verkürzungsfaktor für das Pegasus-Verfahren:

m(f2, fz): return f2 ÷ (f2 + fz)

Der eigentliche, rekursive Algorithmus:

betterFalsePosition(x1, x2, f1, f2):
  z := x1 − f1 · (x2 − x1) ÷ (f2 − f1) // Näherung für die Nullstelle berechnen
  fz := f(z)

  // Abbruchgrenze unterschritten?: z als Näherung zurückgeben
  if |x2 − x1| < epsx or |fz| < epsf then return z

  // ansonsten, Nullstelle in [f(xz), f(x2)]?: „Links und Rechts“ vertauschen, Nullstelle in [f(xz), f(x2)] suchen
  if fz · f2 < 0 then return betterFalsePosition(x2, z, f2, fz)

  // ansonsten: „verkürzen“ und Nullstelle in [x1, z] suchen
  return betterFalsePosition(x1, z, m(f2, fz) · f1, fz)

Die Methode, mit der das Verfahren für das zu untersuchende Intervall, gestartet wird:

betterFalsePosition(x1, x2): return betterFalsePosition(x1, x2, f(x1), f(x2))

• Die Konvergenz der Verfahren ist superlinear und mit der des Sekantenverfahrens vergleichbar.
• Durch die superlineare, garantierte Konvergenz und den relativ geringen Rechenaufwand je Iteration sind diese Verfahren bei eindimensionalen Problemen in der Regel anderen Verfahren (wie z. B. dem Newton-Verfahren) vorzuziehen.

Die historische Regula falsi findet sich bereits in sehr alten mathematischen Texten, beispielsweise wird sie im Papyrus Rhind (ca. 1550 v. Chr.) angewandt.^[3]

Unter den ältesten erhaltenen Dokumenten, die vom Wissen um die Methode des doppelten falschen Ansetzens zeugen, befindet sich die indisch-mathematische Schrift „Vaishali Ganit“ (ca. 3. Jahrhundert v. Chr.). Der altchinesische mathematische Text Die Neun Kapitel der mathematischen Kunst (200 v. Chr. – 100 n. Chr.) erwähnt den Algorithmus ebenfalls. In diesem Text wurde das Verfahren auf eine lineare Gleichung angewandt, sodass die Lösung direkt, also ohne Iteration, erreicht wurde. Auf den Bagdader Mathematiker, Philosoph und Arzt Qusta ibn Luqa (820–912) geht eine geometrische Begründung der Regula falsi zurück.^[4] Leonardo da Pisa (Fibonacci) beschrieb das Verfahren des doppelten falschen Ansetzens in seinem Buch „Liber Abaci“ (1202 n. Chr.),^[1] angelehnt an eine Methode, die er aus arabischen Quellen gelernt hatte.

Auch Adam Ries kannte die regula falsi und beschrieb die Methode wie folgt:

Die ursprünglichen Schöpfer der entsprechenden numerischen Verfahren sind nicht bekannt. Die Illinois-Methode wurde 1971 veröffentlicht, mit einem Hinweis auf den möglichen Ursprung in den 1950er Jahren im Rechenzentrum der University of Illinois.^[5] Die 1972 öffentlich beschriebene Pegasus-Methode wurde so benannt, weil unbekannte Autoren sie zuvor auf einem Röhrenrechner des Typs Pegasus eingesetzt hatten;^[6] dieser Rechner war von der britischen Firma Ferranti Pegasus ab 1956 ausgeliefert worden.

1. ↑ ^{a b} Leonardo da Pisa: Liber abbaci. 1202, Kapitel 13. De regula elcataym qualiter per ipsam fere omnes erratice questiones soluantur. 
2. ↑ ^{a b} Adam Ries: Rechenung auff der linihen und federn. 1522 (Siehe Matroids Matheplanet: Die regula falsi – Adam Ries’ wichtigste Rechenregel.). 
3. ↑ Arnold Buffum Chase: The Rhind Mathematical Papyrus. Free Translation and Commentary with Selected Photographs Transcriptions, Transliterations and Literal Translations by Arnold Buffum Chase, Editoren: Phillip S. Jones, Bruce E. Meserve, The National Council of Teachers of Mathematics, Classics in Mathematics Education A Series, 1979.
4. ↑ Hans-im-Pech: Mathematik: Die regula falsi – Adam Ries’ wichtigste Rechenregel. In: Matroids Matheplanet – Die Mathe Redaktion. 26. Juni 2007, abgerufen am 31. Oktober 2020. 
5. ↑ M. Dowell, P. Jarratt: A modified regula falsi method for computing the root of an equation. In: BIT Numerical Mathematics. Band 11, Nr. 2. Springer, Juni 1971, ISSN 0006-3835, S. 168–174, doi:10.1007/BF01934364 (springer.com). 
6. ↑ M. Dowell, P. Jarratt: The “Pegasus” method for computing the root of an equation. In: BIT Numerical Mathematics. Band 12, Nr. 4. Elsevier, Dezember 1972, ISSN 0006-3835, S. 503–508, doi:10.1007/BF01932959 (springer.com).